题目内容
已知a=2 -
，b=log2
，c=log23，则（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| A、a＞b＞c |
| B、z＞c＞b |
| C、c＞b＞a |
| D、c＞a＞b |
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用指数函数与对数函数的单调性即可得出．
解答：
解：∵0＜a=2 -
＜1，b=log2
＜0，c=log23＞1，
∴c＞a＞b，
故选：D．
| 1 |
| 3 |
| 1 |
| 3 |
∴c＞a＞b，
故选：D．
点评：本题考查了指数函数与对数函数的单调性，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
集合A={y|y=
，0≤x≤4}，B={x|x2-x＞0}，则A∩B=（ ）
| x |
| A、（-∞，1]∪（2，+∞） |
| B、（-∞，0）∪（1，2） |
| C、∅ |
| D、（1，2] |
若集合A={x|1≤3x≤81}，B={x|log2（x2-x）＞1}，则A∩B=（ ）
| A、（2，4] |
| B、[2，4] |
| C、（-∞，0）∪[0，4] |
| D、（-∞，-1）∪[0，4] |
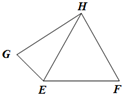已知△EFH是边长为1的正三角形，动点G在平面EFH内．若| EG |
| EF |
| HG |
则
| HG |
| EF |
A、[-1，-
| ||||||
B、[-1，-
| ||||||
C、（-
| ||||||
D、（-
|