题目内容
已知椭圆
+
=1,过右焦点F2的直线l交椭圆于A、B两点,若|AB|=
,求直线l的直线方程.
| x2 |
| 5 |
| y2 |
| 4 |
4
| ||
| 9 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:当AB⊥x轴时,把x=1代入可得
+
=1,解得y,此时|AB|=
≠
,舍去.当AB的斜率存在时,设直线AB的方程为:y=k(x-1),A(x1,y1),B(x2,y2).与椭圆的方程联立可得根与系数的关系,再利用弦长公式解出即可.
| 1 |
| 5 |
| y2 |
| 4 |
8
| ||
| 5 |
4
| ||
| 9 |
解答:
解:c=
=1,∴F2(1,0).
当AB⊥x轴时,把x=1代入可得
+
=1,解得y=±
,此时|AB|=
≠
,舍去.
当AB的斜率存在时,设直线AB的方程为:y=k(x-1),A(x1,y1),B(x2,y2).
联立
,化为(4+5k2)x2-10k2x+5k2-20=0,
∴x1+x2=
,x1x2=
,
∴|AB|=
=
=
,
化为13k2=-14,
∴满足|AB|=
的直线l不存在.
综上可得:满足|AB|=
的直线l不存在.
| 5-4 |
当AB⊥x轴时,把x=1代入可得
| 1 |
| 5 |
| y2 |
| 4 |
4
| ||
| 5 |
8
| ||
| 5 |
4
| ||
| 9 |
当AB的斜率存在时,设直线AB的方程为:y=k(x-1),A(x1,y1),B(x2,y2).
联立
|
∴x1+x2=
| 10k2 |
| 4+4k2 |
| 5k2-20 |
| 4+5k2 |
∴|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[
|
4
| ||
| 9 |
化为13k2=-14,
∴满足|AB|=
4
| ||
| 9 |
综上可得:满足|AB|=
4
| ||
| 9 |
点评:本题考查了直线与椭圆相交问题转化为椭圆的方程联立可得根与系数的关系、弦长公式,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若集合A={x|1≤3x≤81},B={x|log2(x2-x)>1},则A∩B=( )
| A、(2,4] |
| B、[2,4] |
| C、(-∞,0)∪[0,4] |
| D、(-∞,-1)∪[0,4] |
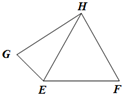 已知△EFH是边长为1的正三角形,动点G在平面EFH内.若
已知△EFH是边长为1的正三角形,动点G在平面EFH内.若| EG |
| EF |
| HG |
则
| HG |
| EF |
A、[-1,-
| ||||||
B、[-1,-
| ||||||
C、(-
| ||||||
D、(-
|
 一几何体三视图为如图所示的三个直角三角形,且该几何体所有棱中最长棱为1,且满足a+
一几何体三视图为如图所示的三个直角三角形,且该几何体所有棱中最长棱为1,且满足a+