题目内容
已知△ABC是边长为2的正三角形，则
•
的值为（ ）
| AB |
| BC |
| A、2 | ||
| B、-2 | ||
C、2
| ||
D、-2
|
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的定义，结合正三角形的定义，注意向量的夹角为π-B，计算即可得到所求值．
解答：
解：由于△ABC是边长为2的正三角形，
则
•
=|
|•|
|•cos（π-B）=-2×2×cos60°
=-4×
=-2．
故选B．
则
| AB |
| BC |
| AB |
| BC |
=-4×
| 1 |
| 2 |
故选B．
点评：本题考查向量的数量积的定义，注意向量夹角的定义是解题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
一几何体三视图为如图所示的三个直角三角形，且该几何体所有棱中最长棱为1，且满足a+
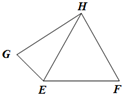已知△EFH是边长为1的正三角形，动点G在平面EFH内．若| EG |
| EF |
| HG |
则
| HG |
| EF |
A、[-1，-
| ||||||
B、[-1，-
| ||||||
C、（-
| ||||||
D、（-
|
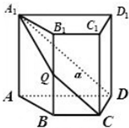如图，四棱柱ABCD-A1B1C1D1中，AA1⊥面ABCD，四边形ABCD为梯形，AD∥BC，且AD=3BC，过A1，C，D三点的平面记为α，BB1与α的交点为Q，则