题目内容
在直角坐标系中,A(-2,0),B(2,0)是两个定点,C(0,p).D(0,q)是两个动点,且pq=3.
(Ⅰ)求直线AC与BD交点的轨迹M的方程;
(Ⅱ)已知点P(1,t)是轨迹M上位于x轴上方的定点,E,F是轨迹M上的两个动点,直线PE与直线PF分别与x轴相交于G、H两点,且∠PGH=∠PHG,求直线EF的斜率.
(Ⅰ)求直线AC与BD交点的轨迹M的方程;
(Ⅱ)已知点P(1,t)是轨迹M上位于x轴上方的定点,E,F是轨迹M上的两个动点,直线PE与直线PF分别与x轴相交于G、H两点,且∠PGH=∠PHG,求直线EF的斜率.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由已知得直线AC的方程,得到p=
,得直线BD的方程,得q=
,再由pq=3得直线AC与BD交点的轨迹M的方程;
(Ⅱ)把点P(1,t)代入M的轨迹方程得t=
.进一步得到P的坐标,设直线PE的斜率为k,写出直线PE方程,联立直线方程与M的轨迹,把E的坐标用k表示,同理把F的坐标用k表示,然后利用两点求斜率公式可得答案.
| 2y |
| x+2 |
| -2y |
| x-2 |
(Ⅱ)把点P(1,t)代入M的轨迹方程得t=
| 3 |
| 2 |
解答:
解:(Ⅰ)由A(-2,0),C(0,p),可得直线AC的方程为
=
,即p=
.
由B(2,0),D(0,q),可得直线BD的方程为
=
,即q=
.
由pq=3,得
•
=3,整理得:
+
=1,
∵pq≠0,∴C,D不与原点重合,即A(-2,0),B(2,0)不在轨迹M上,
∴直线AC与BD交点的轨迹M的方程为
+
=1(y≠0);
(Ⅱ)∵点P(1,t)是轨迹M上位于x轴上方的定点,∴
+
=1,解得t=
.
∴P(1,
),
设直线PE的斜率为k,则直线PE方程为y=k(x-1)+
,代入
+
=1,
得(3+4k2)x2+4k(3-2k)x+4(
-k)2-12=0.
设E(x1,y1),F(x2,y2),
∵P(1,
)在曲线M上,
∴x1=
,y1=kx1+
-k,
又∠PGH=∠PHG,得直线PF的斜率为-k,
同理可得x2=
,y2=-kx2+
+k,
∴直线EF的斜率为kEF=
=
.
∵x1+x2=
,x2-x1=
,
∴kEF=
=
=
=
.
| y-0 |
| p-0 |
| x-(-2) |
| 0-(-2) |
| 2y |
| x+2 |
由B(2,0),D(0,q),可得直线BD的方程为
| y-0 |
| q-0 |
| x-2 |
| 0-2 |
| -2y |
| x-2 |
由pq=3,得
| 2y |
| x+2 |
| -2y |
| x-2 |
| x2 |
| 4 |
| y2 |
| 3 |
∵pq≠0,∴C,D不与原点重合,即A(-2,0),B(2,0)不在轨迹M上,
∴直线AC与BD交点的轨迹M的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)∵点P(1,t)是轨迹M上位于x轴上方的定点,∴
| 1 |
| 4 |
| t2 |
| 3 |
| 3 |
| 2 |
∴P(1,
| 3 |
| 2 |
设直线PE的斜率为k,则直线PE方程为y=k(x-1)+
| 3 |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
得(3+4k2)x2+4k(3-2k)x+4(
| 3 |
| 2 |
设E(x1,y1),F(x2,y2),
∵P(1,
| 3 |
| 2 |
∴x1=
4(
| ||
| 3+4k2 |
| 3 |
| 2 |
又∠PGH=∠PHG,得直线PF的斜率为-k,
同理可得x2=
4(
| ||
| 3+4k2 |
| 3 |
| 2 |
∴直线EF的斜率为kEF=
| y2-y1 |
| x2-x1 |
| -k(x1+x2)+2k |
| x2-x1 |
∵x1+x2=
| 8k2-6 |
| 4k2+3 |
| 24k |
| 4k2+3 |
∴kEF=
| y2-y1 |
| x2-x1 |
| -k(x1+x2)+2k |
| x2-x1 |
| -k(8k2-6)+24(4k2+3) |
| 24k |
| 1 |
| 2 |
点评:本题考查了曲线方程的求法,考查了直线与圆锥曲线的关系,直线与圆锥曲线的位置关系的应用,常采用直线与曲线联立,根据方程的根与系数的关系求解,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
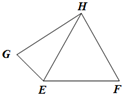 已知△EFH是边长为1的正三角形,动点G在平面EFH内.若
已知△EFH是边长为1的正三角形,动点G在平面EFH内.若| EG |
| EF |
| HG |
则
| HG |
| EF |
A、[-1,-
| ||||||
B、[-1,-
| ||||||
C、(-
| ||||||
D、(-
|
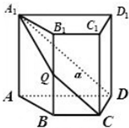 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则| B1Q |
| QB |
| A、1 | ||
| B、2 | ||
| C、3 | ||
D、与
|
设函数y=f(x)在R上有定义,对于任一给定的正数p,定义函数fp(x)=
,则称函数fp(x)为f(x)的“p界函数”,若给定函数f(x)=x2-2x-2,p=1,则下列结论成立的是( )
|
| A、fp[f(0)]=f[fp(0)] |
| B、fp[f(1)]=f[fp(1)] |
| C、fp[f(2)]=fp[fp(2)] |
| D、f[f(-2)]=fp[fp(-2)] |
 如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )
如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )