题目内容
设平面向量
=(
,-
),
=(
,
)若存在不同时为零的两个实数s、t及实数k,使
=
+(t2-k)
,
=-s
+t
,且
⊥
(1)求函数关系式S=f(t);
(2)若函数S=f(t)在[1,+∞]上是单调函数,求k的取值范围.
| a |
| ||
| 2 |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
(1)求函数关系式S=f(t);
(2)若函数S=f(t)在[1,+∞]上是单调函数,求k的取值范围.
考点:平面向量数量积的运算,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:平面向量及应用
分析:(1)首先根据向量的坐标求出向量的数量积和向量的模,然后利用向量垂直的充要条件求出函数的关系式.
(2)利用定义法证明函数的单调性,然后根据定义域求出函数关系式的值域,最后求出参数的取值范围.
(2)利用定义法证明函数的单调性,然后根据定义域求出函数关系式的值域,最后求出参数的取值范围.
解答:
解:(1)已知向量
=(
,-
),
=(
,
)
所以:
•
=
•
-
•
=0,|
|=|
|=1
则:
=
+(t2-k)
=,
=-s
+t
,
由于
⊥
所以:
•
=-s
2+t
•
-s(t2-k)
•
+t(t2-k)
2=0
整理得:s=f(t)=t3-kt
(2)设:t1>t2≥1
所以:f(t1)-f(t2)=t13-kt1-t23+kt2
=(t1-t2)(t12+t1t2+t22-k)
由于函数S=f(t)在[1,+∞]上是单调函数,
所以:t12+t1t2+t22-k>0
即:t12+t1t2+t22>k
由于t12+t1t2+t22>3
所以:k≤3
即k的取值范围为:k≤3.
| a |
| ||
| 2 |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| ||
| 2 |
所以:
| a |
| b |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
则:
| x |
| a |
| b |
| y |
| a |
| b |
由于
| x |
| y |
所以:
| x |
| y |
| a |
| a |
| b |
| a |
| b |
| b |
整理得:s=f(t)=t3-kt
(2)设:t1>t2≥1
所以:f(t1)-f(t2)=t13-kt1-t23+kt2
=(t1-t2)(t12+t1t2+t22-k)
由于函数S=f(t)在[1,+∞]上是单调函数,
所以:t12+t1t2+t22-k>0
即:t12+t1t2+t22>k
由于t12+t1t2+t22>3
所以:k≤3
即k的取值范围为:k≤3.
点评:本题考查的知识要点:向量的运算,向量垂直的充要条件的应用,向量数量积和向量的模的应用,函数的单调性的应用.属于中等题型.

练习册系列答案
相关题目
集合A={y|y=
,0≤x≤4},B={x|x2-x>0},则A∩B=( )
| x |
| A、(-∞,1]∪(2,+∞) |
| B、(-∞,0)∪(1,2) |
| C、∅ |
| D、(1,2] |
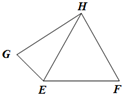 已知△EFH是边长为1的正三角形,动点G在平面EFH内.若
已知△EFH是边长为1的正三角形,动点G在平面EFH内.若| EG |
| EF |
| HG |
则
| HG |
| EF |
A、[-1,-
| ||||||
B、[-1,-
| ||||||
C、(-
| ||||||
D、(-
|
设函数y=f(x)在R上有定义,对于任一给定的正数p,定义函数fp(x)=
,则称函数fp(x)为f(x)的“p界函数”,若给定函数f(x)=x2-2x-2,p=1,则下列结论成立的是( )
|
| A、fp[f(0)]=f[fp(0)] |
| B、fp[f(1)]=f[fp(1)] |
| C、fp[f(2)]=fp[fp(2)] |
| D、f[f(-2)]=fp[fp(-2)] |





 一几何体三视图为如图所示的三个直角三角形,且该几何体所有棱中最长棱为1,且满足a+
一几何体三视图为如图所示的三个直角三角形,且该几何体所有棱中最长棱为1,且满足a+