题目内容
已知f(x)=x3+ax2的图象为曲线C,M,N是曲线C上的不同点,曲线C在M,N处的切线斜率均为k.
(1)若a=3,函数g(x)=
的图象在点x1,x2处的切线互相垂直,求|x1-x2|的最小值;
(2)若MN的方程为x+y+1=0,求k的值.
(1)若a=3,函数g(x)=
| f(x) |
| x |
(2)若MN的方程为x+y+1=0,求k的值.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由题意求出g(x)的解析式,求出其导函数,结合g(x)的图象在点x1,x2处的切线互相垂直把x2用x1表示,代入|x1-x2|后利用基本不等式求最值;
(2)设M(m,m3+am2),N(n,n3+an2)(m≠n),求出原函数的导函数,由曲线C在M,N处的切线斜率均为k得到3m2+2am=3n2+2an,进一步得到m+n=-
a,再由M,N在x+y+1=0上,可得m3+am2+m+1=0,n3+an2+n+1=0,即(m+n)[(m+n)2-3mn]+a[(m+n)2-2mn]+m+n+2=0,联立m+n=-
a求得a的值,进一步得到m3-3m2+m+1=0,由此求得m的值,同理求得n的值,说明m,n均是方程x2-2x-1=0的根.由k=f'(m)求得k值.
(2)设M(m,m3+am2),N(n,n3+an2)(m≠n),求出原函数的导函数,由曲线C在M,N处的切线斜率均为k得到3m2+2am=3n2+2an,进一步得到m+n=-
| 2 |
| 3 |
| 2 |
| 3 |
解答:
解:(1)a=3时,f(x)=x3+3x2,g(x)=
=x2+3x,
∴g'(x)=2x+3,
∵g(x)的图象在点x1,x2处的切线互相垂直,∴(2x1+3)(2x2+3)=-1,则x2=-
•
-
,
∴|x1-x2|=|x1+
+
•
|=|x1+
|+
•
≥1,当且仅当x1=-2,x2=-1或x1=-1,x2=-2时取最小值1;
(2)设M(m,m3+am2),N(n,n3+an2)(m≠n),f'(x)=3x2+2ax,
∵3m2+2am=3n2+2an,
∴m+n=-
a,
又∵M,N在x+y+1=0上,
∴m3+am2+m+1=0,n3+an2+n+1=0,
∴m3+n3+a(m2+n2)+m+n+2=0.
即(m+n)[(m+n)2-3mn]+a[(m+n)2-2mn]+m+n+2=0,
将m+n=-
a代入上式得2a3-9a+27=0,
即2a3-9a+27=(a+3)(2a2-6a+9)=0,解得a=-3.
∴m3-3m2+m+1=0,
则m3-3m2+m+1=(m-1)(m2-2m-1)=0,
解得m=1或m=1±
;
同理n=1或n=1±
.
∵m+n=-
a=2,且m≠n,
∴m,n均满足方程x2-2x-1=0.
故k=f'(m)=3m2-6m=3(m2-2m)=3.
| f(x) |
| x |
∴g'(x)=2x+3,
∵g(x)的图象在点x1,x2处的切线互相垂直,∴(2x1+3)(2x2+3)=-1,则x2=-
| 1 |
| 4 |
| 1 | ||
x1+
|
| 3 |
| 2 |
∴|x1-x2|=|x1+
| 3 |
| 2 |
| 1 |
| 4 |
| 1 | ||
x1+
|
| 3 |
| 2 |
| 1 |
| 4 |
| 1 | ||
|x1+
|
(2)设M(m,m3+am2),N(n,n3+an2)(m≠n),f'(x)=3x2+2ax,
∵3m2+2am=3n2+2an,
∴m+n=-
| 2 |
| 3 |
又∵M,N在x+y+1=0上,
∴m3+am2+m+1=0,n3+an2+n+1=0,
∴m3+n3+a(m2+n2)+m+n+2=0.
即(m+n)[(m+n)2-3mn]+a[(m+n)2-2mn]+m+n+2=0,
将m+n=-
| 2 |
| 3 |
即2a3-9a+27=(a+3)(2a2-6a+9)=0,解得a=-3.
∴m3-3m2+m+1=0,
则m3-3m2+m+1=(m-1)(m2-2m-1)=0,
解得m=1或m=1±
| 2 |
同理n=1或n=1±
| 2 |
∵m+n=-
| 2 |
| 3 |
∴m,n均满足方程x2-2x-1=0.
故k=f'(m)=3m2-6m=3(m2-2m)=3.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,训练了利用基本不等式求最值,考查了数学转化思想方法,考查了方程思想的应用,是压轴题.

练习册系列答案
相关题目
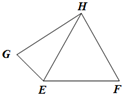 已知△EFH是边长为1的正三角形,动点G在平面EFH内.若
已知△EFH是边长为1的正三角形,动点G在平面EFH内.若| EG |
| EF |
| HG |
则
| HG |
| EF |
A、[-1,-
| ||||||
B、[-1,-
| ||||||
C、(-
| ||||||
D、(-
|
 如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,SA=a且
如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,SA=a且



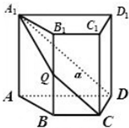 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则