题目内容
19．如图是某几何体的三视图，则其体积是（ ）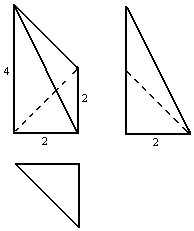
| A． | 8 | B． | $\frac{8}{3}$ | C． | 4 | D． | $\frac{4}{3}$ |
分析 根据四棱锥的三视图，得直观图是三棱锥，底面为直角三角形，直角边分别为4，2$\sqrt{2}$，棱锥的高为$\sqrt{2}$，即可求出它的体积．
解答 解：根据三视图，得直观图是三棱锥，底面为直角三角形，直角边分别为4，2$\sqrt{2}$，棱锥的高为$\sqrt{2}$；
所以，该棱锥的体积为
V=$\frac{1}{3}$S底面积•h=$\frac{1}{3}$×$\frac{1}{2}$×4×2$\sqrt{2}$×$\sqrt{2}$=$\frac{8}{3}$．
故选：B．
点评 本题考查了利用三视图求体积的应用问题，解题的关键是根据三视图得出几何体的结构特征，是基础题目．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
7．若点P的直角坐标为（1，$\sqrt{3}$），则它的极坐标可以是（ ）
| A． | （2，-$\frac{π}{3}$） | B． | （2，$\frac{4π}{3}$） | C． | （2，$\frac{π}{3}$） | D． | （2，-$\frac{4π}{3}$） |
4．在面积为1的△ABC的边AB上任取一点P，则△PBC的面积不小于$\frac{1}{3}$的概率是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{4}$ |