题目内容
7.若点P的直角坐标为(1,$\sqrt{3}$),则它的极坐标可以是( )| A. | (2,-$\frac{π}{3}$) | B. | (2,$\frac{4π}{3}$) | C. | (2,$\frac{π}{3}$) | D. | (2,-$\frac{4π}{3}$) |
分析 利用直角坐标和极坐标互化公式直接求解.
解答 解:∵点P的直角坐标为(1,$\sqrt{3}$),
∴$ρ=\sqrt{1+3}$=2,
tanθ=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$,
∴θ=$\frac{π}{3}$.
∴点P的极坐标为(2,$\frac{π}{3}$).
故选:C.
点评 本题考查点的极坐标的求法,是基础题,解题时要认真审题,注意直角坐标和极坐标互化公式的合理运用.

练习册系列答案
相关题目
17.执行如图所示的程序框图,则输出的x等于( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
18.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据如表所示:
(1)求出y关于x的线性回归方程;
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
| 价格x/元 | 14 | 16 | 18 | 20 | 22 |
| 需求量y/件 | 56 | 50 | 3 | 1 | 37 |
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
15.过正三棱柱底面一边所作的正三棱柱的截面是( )
| A. | 三角形 | B. | 三角形或梯形 | ||
| C. | 不是梯形的四边形 | D. | 梯形 |
2.已知$A=\left\{{x\left|{{3^x}<1}\right.}\right\},B=\left\{{x\left|{y=\sqrt{x+3}}\right.}\right\}$,则A∩B=( )
| A. | [-3,0) | B. | [-3,0] | C. | (0,+∞) | D. | [-3,+∞) |
12.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么|$\overrightarrow{a}$-2$\overrightarrow{b}$|等于( )
| A. | 2 | B. | $4-\sqrt{3}$ | C. | $\sqrt{13}$ | D. | $\sqrt{3}$ |
19.如图是某几何体的三视图,则其体积是( )
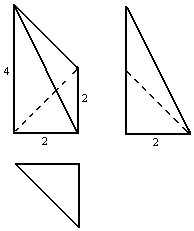

| A. | 8 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
16.同学聚会上,某同学从《爱你一万年》,《十年》,《父亲》,《单身情歌》四首歌选出两首歌进行表演,则《爱你一万年》未选取的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
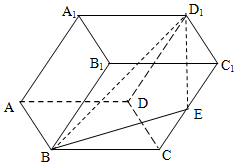 已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,
已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,