题目内容
4.在面积为1的△ABC的边AB上任取一点P,则△PBC的面积不小于$\frac{1}{3}$的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
分析 首先分析题目求在面积为1的△ABC的边AB上任取一点P,则△PBC的面积不小于$\frac{1}{3}$的概率,即可考虑画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是什么.再根据几何关系求解出它们的比例即可.
解答  解:记事件A={△PBC的面积大于等于$\frac{1}{3}$},
解:记事件A={△PBC的面积大于等于$\frac{1}{3}$},
基本事件空间是线段AB的长度,(如图)
因为${S}_{△PBC}≥\frac{1}{3}$,则有PE$≥\frac{1}{3}AD$;
因为PE平行AD则由三角形的相似性BP$≥\frac{1}{3}AB$;
所以,事件A的几何度量为线段AP的长度,
因为AP=$\frac{2}{3}$AB,
所以P(A)=$\frac{AP}{AB}$=$\frac{2}{3}$.
故选A.
点评 解决有关几何概型的问题的关键是认清基本事件空间是指面积还是长度或体积,并且熟练记忆有关的概率公式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
15.过正三棱柱底面一边所作的正三棱柱的截面是( )
| A. | 三角形 | B. | 三角形或梯形 | ||
| C. | 不是梯形的四边形 | D. | 梯形 |
12.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么|$\overrightarrow{a}$-2$\overrightarrow{b}$|等于( )
| A. | 2 | B. | $4-\sqrt{3}$ | C. | $\sqrt{13}$ | D. | $\sqrt{3}$ |
19.如图是某几何体的三视图,则其体积是( )
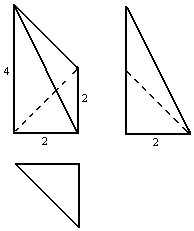

| A. | 8 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
16.同学聚会上,某同学从《爱你一万年》,《十年》,《父亲》,《单身情歌》四首歌选出两首歌进行表演,则《爱你一万年》未选取的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
13.“x>-2”是“x2<4”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.小品类是春节文艺晚会的重要节目,一调查机构为研究“喜欢收看春节文艺晚会小品类节目与地域文化是否有关”,在南北方不同地域随机抽取了100名市民进行调查,发现被调查对象的北方人有40名喜欢收看,有15名不喜欢收看;调查对象的南方人有20名喜欢收看,有25名不喜欢收看
(1)在被调查对象中,喜欢收看春节文艺晚会小品类节目的人数占各自地域的比例分别是多少?并初步判断喜欢收看春节文艺晚会小品类节目与地域是否有关?
(2)试根据题设数据完成2X2列联表,并判断是否有99.5%的把握认为喜欢收看春节文艺晚会小品类节目与地域文化有关
参考数据公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$
临界值:
(1)在被调查对象中,喜欢收看春节文艺晚会小品类节目的人数占各自地域的比例分别是多少?并初步判断喜欢收看春节文艺晚会小品类节目与地域是否有关?
(2)试根据题设数据完成2X2列联表,并判断是否有99.5%的把握认为喜欢收看春节文艺晚会小品类节目与地域文化有关
参考数据公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},n=a+b+c+d$
临界值:
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |