题目内容
11.已知数列{an}满足a1=-40,且nan+1-(n+1)an=2n2+2n,则an取最小值时n的值为10或11.分析 nan+1-(n+1)an=2n2+2n,化为$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=2,利用等差数列的通项公式可得an,再利用二次函数的单调性即可得出.
解答 解:∵nan+1-(n+1)an=2n2+2n,∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=2,
∴数列{$\frac{{a}_{n}}{n}$}是等差数列,首项为-40,公差为2.
∴$\frac{{a}_{n}}{n}$=-40+2(n-1),化为:an=2n2-42n=2$(n-\frac{21}{2})^{2}$-$\frac{441}{2}$.
则an取最小值时n的值为10或11.
故答案为:10或11.
点评 本题考查了等差数列的通项公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.对函数f(x)=$\left\{\begin{array}{l}{-x+1,x>0}\\{-x-1,x≤0}\end{array}\right.$性质,下列叙述正确为( )
| A. | 奇函数 | B. | 减函数 | ||
| C. | 既是奇函数又是减函数 | D. | 不是奇函数也不是减函数 |
2.已知$A=\left\{{x\left|{{3^x}<1}\right.}\right\},B=\left\{{x\left|{y=\sqrt{x+3}}\right.}\right\}$,则A∩B=( )
| A. | [-3,0) | B. | [-3,0] | C. | (0,+∞) | D. | [-3,+∞) |
19.如图是某几何体的三视图,则其体积是( )
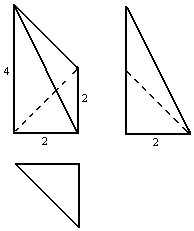

| A. | 8 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
16.同学聚会上,某同学从《爱你一万年》,《十年》,《父亲》,《单身情歌》四首歌选出两首歌进行表演,则《爱你一万年》未选取的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
3.已知函数f(x)(x∈R)的图象上任一点(x0,y0)处的切线方程为y-y0=(x0-2)(x02-1)(x-x0),那么函数f(x)的单调递减区间是( )
| A. | [-1,+∞) | B. | (-∞,2] | C. | (-∞,-1)和(1,2) | D. | [2,+∞) |
20.《中华人民共和国个人所得税法》规定:2011年9月1 日开始个人所得税起征点由原来的2000元提高到3500元.也就是说原来月收人超过2000元的部分需要纳税,2011年9月1日开始超过3500元的部分需要纳税,若税法修改前后超过部分的税率相同.按如表分段计税
某职工2011年5月交纳个人所得税295元,在收人不变的情况下,2011年10月该职工需交纳个人所得税145元.
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过1500元的部分 | 3 |
| 2 | 超过1500不超过4500元的部分 | 10 |
| 3 | 超过4500不超过9000元的部分 | 20 |