题目内容
14.已知函数f(x)=x3-3x.(Ⅰ)若曲线y=f(x)与直线y=m有且只有一个公共点,求m的取值范围;
(Ⅱ)过点P(2,-6)作曲线y=f(x)的切线,求此切线的方程.
分析 (Ⅰ)先求出其导函数,利用其导函数求出其极值,求出m的范围即可;
(II)先根据解析式设出切点坐标,利用点斜式和f′(x)求出切线方程,再把点P(2,-6)代入切线方程,求出切点的横坐标x0,再代入切线方程化简即可.
解答 解:(Ⅰ)令f′(x)=3x2-3=0,得x=±1,
可求得f(x)的极大值为f(-1)=2,极小值为f(1)=-2,
故当满足-2<m<2时,恰有三个不同公共点.
(II)∵f(x)=x3-3x,∴设切点为Q(x0,x03-3x0),
则所求切线方程为:y-(x03-3x0)=(3x02-3)(x-x0)①,
∵切线过点P(2,-6),∴-6-(x03-3x0)=(3x02-3)(2-x0),
解得x0=0或x0=3,代入①化简得y=-3x或y+6=24(x-2),
∴切线方程为3x+y=0或24x-y-54=0.
点评 本题考查了导数的几何意义,以及切点在曲线和切线上的应用,注意“在某点处的切线”和“过某点处的切线”的区别和求法.

练习册系列答案
相关题目
5.将原油精炼为汽油,柴油等各种不同产品,需要对原油进行冷却和加热.如果第xh时,原油的温度(单位:°C)为$y=f(x)=\root{3}{{\frac{3x}{4e}}}(e=2.71828…)$,则第6h时,原油温度的瞬时变化率为( )
| A. | $\root{3}{{\frac{9}{2e}}}$ | B. | $\frac{1}{6}\root{3}{{\frac{1}{6e}}}$ | C. | $\frac{1}{9}\root{3}{{\frac{{4{e^2}}}{3}}}$ | D. | 以上答案均不对 |
2.已知$A=\left\{{x\left|{{3^x}<1}\right.}\right\},B=\left\{{x\left|{y=\sqrt{x+3}}\right.}\right\}$,则A∩B=( )
| A. | [-3,0) | B. | [-3,0] | C. | (0,+∞) | D. | [-3,+∞) |
9.设公比大于零的等比数列{an}的前n项和为Sn,且a1=1,S4=5S2,数列{an}的通项公式( )
| A. | an=2n-1 | B. | an=3n | C. | 2 | D. | an=5n |
19.如图是某几何体的三视图,则其体积是( )
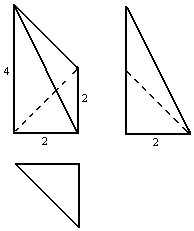

| A. | 8 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
3.已知函数f(x)(x∈R)的图象上任一点(x0,y0)处的切线方程为y-y0=(x0-2)(x02-1)(x-x0),那么函数f(x)的单调递减区间是( )
| A. | [-1,+∞) | B. | (-∞,2] | C. | (-∞,-1)和(1,2) | D. | [2,+∞) |