题目内容
9.已知函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$.(1)求f[f(0)+4]的值;
(2)求证:f(x)在R上是增函数.
分析 (1)根据题意,由函数的解析式可得f(0)的值,即可得f(0)+4的值,进而代入函数解析式计算可得f[f(0)+4]的值;
(2)由作差法证明:设x1,x2∈R且x1<x2,化简并分析f(x1)-f(x2)的符号,即可得证明.
解答 解:(1)根据题意,函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,
则f(0)=$\frac{{2}^{0}-1}{{2}^{0}+1}$=0,∴f[f(0)+4]=f(4)=$\frac{{2}^{4}-1}{{2}^{4}+1}$=$\frac{15}{17}$.
(2)证明 设x1,x2∈R且x1<x2,则${2^{x_2}}$>${2^{x_1}}$>0,${2^{x_2}}$-${2^{x_1}}$>0,
f(x1)-f(x2)=($\frac{{2}^{{x}_{1}}-1}{{2}^{{x}_{1}}+1}$)-($\frac{{2}^{{x}_{2}}-1}{{2}^{{x}_{2}}+1}$)=-$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$<0,
即f(x1)<f(x2),所以f(x)在R上是增函数.
点评 本题考查函数单调性的判定、证明,关键是掌握定义法证明函数单调性的方法.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20.一个几何体的三视图如图所示,则该几何体的体积为( )
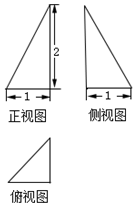

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
17.执行如图所示的程序框图,则输出的x等于( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
1.对函数f(x)=$\left\{\begin{array}{l}{-x+1,x>0}\\{-x-1,x≤0}\end{array}\right.$性质,下列叙述正确为( )
| A. | 奇函数 | B. | 减函数 | ||
| C. | 既是奇函数又是减函数 | D. | 不是奇函数也不是减函数 |
18.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据如表所示:
(1)求出y关于x的线性回归方程;
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
| 价格x/元 | 14 | 16 | 18 | 20 | 22 |
| 需求量y/件 | 56 | 50 | 3 | 1 | 37 |
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
19.如图是某几何体的三视图,则其体积是( )
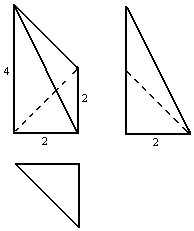

| A. | 8 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |