题目内容
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A、y=log2|x| | ||
| B、y=cos2x | ||
C、y=
| ||
D、y=log2
|
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:分别判断函数的奇偶性和单调性即可得到结论.
解答:
解:A.y=log2|x|为偶函数,当x>0,y=log2|x|=y=log2x单调递增,满足条件.
B.y=cos2x为偶函数,但在(1,2)上不单调,不满足条件.
C.f(-x)=
=-
=-f(x)为奇函数,不满足条件.
D.f(-x)=log2
=log2(
)-1=-log2
=-f(x)为奇函数.不满足条件.
故选:A.
B.y=cos2x为偶函数,但在(1,2)上不单调,不满足条件.
C.f(-x)=
| 2-x-2x |
| 2 |
| 2x-2-x |
| 2 |
D.f(-x)=log2
| 2+x |
| 2-x |
| 2-x |
| 2+x |
| 2-x |
| 2+x |
故选:A.
点评:本题主要考查函数奇偶性和单调性的判断,要求掌握常见函数的奇偶性和单调性的性质.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
复数z=1+i,则
+
对应的点所在的象限为( )
| 1 |
| z |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
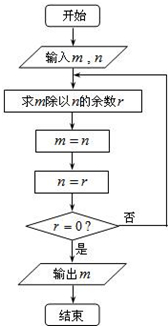 如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )
如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )| A、2010 | B、1541 |
| C、134 | D、67 |
一算法的程序框图如右图所示,若输出的y=
,则输入的x可能为( )

| 1 |
| 2 |

| A、-1 | B、0 | C、1 | D、5 |
等差数列x1,x2,x3…x9的公差为1,随机变量ξ等可能的取值x1,x2,x3…x9,则方差D(ξ)为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
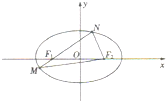 如图,椭圆E:
如图,椭圆E: