题目内容
已知A,B是抛物线W:y=x2上的两个点,点A的坐标为(1,1),直线AB的斜率为k(k>0).设抛物线W的焦点在直线AB的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且AB⊥AC,过B,C两点分别作W的切线,记两切线的交点为D.判断四边形ABDC是否为梯形,并说明理由.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且AB⊥AC,过B,C两点分别作W的切线,记两切线的交点为D.判断四边形ABDC是否为梯形,并说明理由.
考点:直线与圆锥曲线的综合问题
专题:
分析:(Ⅰ)求出抛物线y=x2的焦点,得直线AB的方程为y-1=k(x-1),求出直线AB与y轴相交于点(0,1-k),利用抛物线W的焦点在直线AB的下方,即可求k的取值范围;
(Ⅱ)利用反证法,假设四边形ABDC为梯形,求出B、C处的切线斜率,分类讨论,建立方程,即可得出结论.
(Ⅱ)利用反证法,假设四边形ABDC为梯形,求出B、C处的切线斜率,分类讨论,建立方程,即可得出结论.
解答:
(Ⅰ)解:抛物线y=x2的焦点为(0,
).…(1分)
由题意,得直线AB的方程为y-1=k(x-1),…(2分)
令x=0,得y=1-k,即直线AB与y轴相交于点(0,1-k).…(3分)
∵抛物线W的焦点在直线AB的下方,
∴1-k>
,
解得k<
.…(5分)
∵k>0,
∴0<k<
.…(5分)
(Ⅱ)解:结论:四边形ABDC不可能为梯形.…(6分)
理由如下:
假设四边形ABDC为梯形.…(7分)
由题意,设B(x1,x12),C(x2,x22),D(x3,y3),
联立方程
消去y,得x2-kx+k-1=0,
由韦达定理,得1+x1=k,∴x1=k-1.…(8分)
同理,得x2=-
-1.…(9分)
对函数y=x2求导,得y′=2x,
∴抛物线y=x2在点B处的切线BD的斜率为2x1=2k-2,…(10分)
抛物线y=x2在点C处的切线CD的斜率为2x2=-
-2.…(11分)
由四边形ABDC为梯形,得AB∥CD或AC∥BD.
若AB∥CD,则k=-
-2,即k2+2k+2=0,
∵方程k2+2k+2=0无解,∴AB与CD不平行.…(12分)
若AC∥BD,则-
=2k-2,即2k2-2k+1=0,
∵方程2k2-2k+1=0无解,∴AC与BD不平行.…(13分)
∴四边形ABDC不是梯形,与假设矛盾.
同理AD∥BC也不成立,
因此四边形ABDC不可能为梯形.…(14分)
| 1 |
| 4 |
由题意,得直线AB的方程为y-1=k(x-1),…(2分)
令x=0,得y=1-k,即直线AB与y轴相交于点(0,1-k).…(3分)
∵抛物线W的焦点在直线AB的下方,
∴1-k>
| 1 |
| 4 |
解得k<
| 3 |
| 4 |
∵k>0,
∴0<k<
| 3 |
| 4 |
(Ⅱ)解:结论:四边形ABDC不可能为梯形.…(6分)
理由如下:
假设四边形ABDC为梯形.…(7分)
由题意,设B(x1,x12),C(x2,x22),D(x3,y3),
联立方程
|
消去y,得x2-kx+k-1=0,
由韦达定理,得1+x1=k,∴x1=k-1.…(8分)
同理,得x2=-
| 1 |
| k |
对函数y=x2求导,得y′=2x,
∴抛物线y=x2在点B处的切线BD的斜率为2x1=2k-2,…(10分)
抛物线y=x2在点C处的切线CD的斜率为2x2=-
| 2 |
| k |
由四边形ABDC为梯形,得AB∥CD或AC∥BD.
若AB∥CD,则k=-
| 2 |
| k |
∵方程k2+2k+2=0无解,∴AB与CD不平行.…(12分)
若AC∥BD,则-
| 1 |
| k |
∵方程2k2-2k+1=0无解,∴AC与BD不平行.…(13分)
∴四边形ABDC不是梯形,与假设矛盾.
同理AD∥BC也不成立,
因此四边形ABDC不可能为梯形.…(14分)
点评:本题考查抛物线的定义与方程,考查抛物线的切线方程,考查学生的计算能力,考查反证法,属于中档题.

练习册系列答案
相关题目
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A、y=log2|x| | ||
| B、y=cos2x | ||
C、y=
| ||
D、y=log2
|
阅读如图所示程序框图,运行相应的程序,输出s的值等于( )
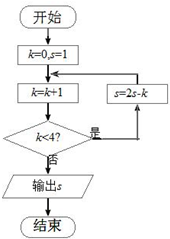

| A、-3 | B、-10 | C、0 | D、-2 |
 如图,抛物线C的顶点为O(0,0),焦点在y轴上,抛物线上的点(x0,1)到焦点的距离为2.
如图,抛物线C的顶点为O(0,0),焦点在y轴上,抛物线上的点(x0,1)到焦点的距离为2.
