题目内容
等差数列x1,x2,x3…x9的公差为1,随机变量ξ等可能的取值x1,x2,x3…x9,则方差D(ξ)为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等差数列的性质,极差、方差与标准差
专题:
分析:等差数列x1,x2,x3…x9的公差为1,求出
=x1+4,由此利用方差公式能求出结果.
. |
| x |
解答:
解:等差数列x1,x2,x3…x9的公差为1,
∴
=
(9x1+
×1)=x1+4,
∴数据x1,x2,x3…x9为样本,
此样本的方差:
D(ξ)=
[(-4)2+(-3)2+(-2)2+(-1)2+02+12+22+32+42]=
.
故选:B.
∴
. |
| x |
| 1 |
| 9 |
| 9×8 |
| 2 |
∴数据x1,x2,x3…x9为样本,
此样本的方差:
D(ξ)=
| 1 |
| 9 |
| 20 |
| 3 |
故选:B.
点评:本题考查样本数据方差的计算,灵活运用等差数列的性质是解答该题的关键,是中档题.

练习册系列答案
相关题目
定义:如果函数y=f(x)在区间[a,b]上存在x1,x2(a<x1<x2<b),满足f′(x1)=
,f′(x2)=
,则称函数y=f(x)在区间[a,b]上的一个双中值函数,已知函数f(x)=
x3-x2+a是区间[0,a]上的双中值函数,则实数a的取值范围是( )
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
| 1 |
| 3 |
A、(0,
| ||
B、(
| ||
C、(
| ||
| D、(1,3) |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A、y=log2|x| | ||
| B、y=cos2x | ||
C、y=
| ||
D、y=log2
|
若复数z满足:iz=3+4i,则|z|=( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、5 |
阅读如图所示程序框图,运行相应的程序,输出s的值等于( )
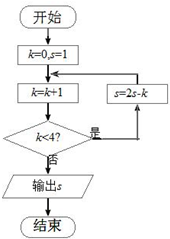

| A、-3 | B、-10 | C、0 | D、-2 |
