题目内容
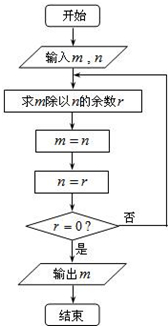如图所示的程序框图描述的算法称为欧几里得辗转相除法，若输入m=2010，n=1541，则输出的m的值为（ ）| A、2010 | B、1541 |
| C、134 | D、67 |
考点：程序框图
专题：算法和程序框图
分析：程序的运行功能是求m=2010，n=1541的最大公约数，根据辗转相除法可得m的值．
解答：
解：由程序框图知：程序的运行功能是求m=2010，n=1541的最大公约数，
∵2010=1541+469；
1541=3×469+134；
469=3×134+67；
134=2×67+0；
∴此时m=67．∴输出m的值为67．
故选：D．
∵2010=1541+469；
1541=3×469+134；
469=3×134+67；
134=2×67+0；
∴此时m=67．∴输出m的值为67．
故选：D．
点评：本题考查了辗转相除法的程序框图，掌握辗转相除法的操作流程是关键．
练习册系列答案
相关题目
复数z=
（i是虚数单位）在复平面内的对应点位于（ ）
| ||
1-
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
定义：如果函数y=f（x）在区间[a，b]上存在x1，x2（a＜x1＜x2＜b），满足f′（x1）=
，f′（x2）=
，则称函数y=f（x）在区间[a，b]上的一个双中值函数，已知函数f（x）=
x3-x2+a是区间[0，a]上的双中值函数，则实数a的取值范围是（ ）
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
| 1 |
| 3 |
A、（0，
| ||
B、（
| ||
C、（
| ||
| D、（1，3） |
函数f（x）=2x2-mx+5，当x∈[-1，+∞）时是增函数，当x∈（-∞，-1]时是减函数，则f（-2）等于（ ）
| A、5 | B、7 |
| C、9 | D、由m的值而定的常数 |
下列函数中，既是偶函数，又在区间（1，2）内是增函数的为（ ）
| A、y=log2|x| | ||
| B、y=cos2x | ||
C、y=
| ||
D、y=log2
|
阅读如图所示程序框图，运行相应的程序，输出s的值等于（ ）
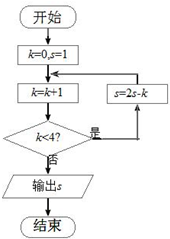
| A、-3 | B、-10 | C、0 | D、-2 |