题目内容
已知幂函数的图象f（x）=x m2-2m-3（m∈Z）与x轴、y轴均无公共点，且其图象关于y轴对称，求f（x）的解析式．
考点：幂函数的概念、解析式、定义域、值域
专题：函数的性质及应用
分析：幂函数的图象f（x）=x m2-2m-3（m∈Z）与x轴、y轴均无公共点，且其图象关于y轴对称，可得m2-2m-3＜0且m2-2m-3为偶数．解出即可．
解答：
解：∵幂函数的图象f（x）=x m2-2m-3（m∈Z）与x轴、y轴均无公共点，且其图象关于y轴对称，
∴m2-2m-3≤0且m2-2m-3为偶数．
解得-1≤m≤3，取m=1时，m2-2m-3=-4；取m=-1，3时，m2-2m-3=0．
∴f（x）=x-4．或f（x）=1（x≠0）．
∴m2-2m-3≤0且m2-2m-3为偶数．
解得-1≤m≤3，取m=1时，m2-2m-3=-4；取m=-1，3时，m2-2m-3=0．
∴f（x）=x-4．或f（x）=1（x≠0）．
点评：本题考查了幂函数的定义、一元二次不等式的解法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
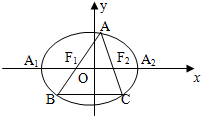如图：A1、A2是椭圆