题目内容
函数y=f（x）的定义域为[-1，2]，则函数g（x）=f（x）-f（-x）的定义域是 ．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据y=f（x）的定义域为[-1，2]，推出函数g（x）=f（x）-f（-x）的自变量x必须满足的不等式组，然后求其解集即可．
解答：
解：∵函数y=f（x）的定义域为[-1，2]，g（x）=f（x）-f（-x）
∴
，
∴-1≤x≤1．
∴函数g（x）=f（x）-f（-x）的定义域[-1，1]．
故答案为：[-1，1]．
∴
|
∴-1≤x≤1．
∴函数g（x）=f（x）-f（-x）的定义域[-1，1]．
故答案为：[-1，1]．
点评：本题主要考查了复合函数的定义域，属常考题，较易．解题的关键是将f（-x）中的-x看做整体在-1与2之间，推出不等式组是解题的关键．
练习册系列答案
相关题目
设集合A={x||x-1|≤2}，B={x|log2x＜2}，则A∪B=（ ）
| A、[-1，3] |
| B、[-1，4） |
| C、（0，3] |
| D、（-∞，4） |
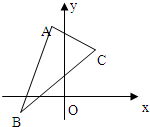如图，已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）