题目内容
过椭圆
+
=1的右焦点F作两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N.
(1)证明:直线MN必过定点,并求此定点;
(2)若弦AB,CD的斜率均存在,求△FMN的面积S的最大值.
| x2 |
| 3 |
| y2 |
| 2 |
(1)证明:直线MN必过定点,并求此定点;
(2)若弦AB,CD的斜率均存在,求△FMN的面积S的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意知F(1,0),当弦AB,CD的斜率均存在时,设AB:y=k(x-1),代入椭圆
+
=1,
得(3k2+2)x2-6k2x+(3k2-6)=0,由韦达定理得M(
,
),将点M中的k换成-
,得到点N(
,
),由此得直线MN过定点(
,0);当弦AB或弦CD的斜率不存在时,直线MN为x轴,过点(
,0),由此能证明直线MN必过定点E(
,0).
(2)由(1)知S△FMN=
|EF|•|yM-yN|=
,由此利用导数性质能求出△FMN的面积的最大值为
.
| x2 |
| 3 |
| y2 |
| 2 |
得(3k2+2)x2-6k2x+(3k2-6)=0,由韦达定理得M(
| 3k2 |
| 3k2+2 |
| -2k |
| 3k2+2 |
| 1 |
| k |
| 3 |
| 2k2+3 |
| 2k |
| 2k2+3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
(2)由(1)知S△FMN=
| 1 |
| 2 |
| |2k(k21)| |
| (3k2+2)(2k2+3) |
| 4 |
| 25 |
解答:
(1)证明:由题意知F(1,0),
①当弦AB,CD的斜率均存在时,设AB的斜率为k,则CD的斜率为-
,
设AB:y=k(x-1),代入椭圆
+
=1,
得(3k2+2)x2-6k2x+(3k2-6)=0,
∴xM=
=
,yM=k(xM-1)=
,
∴M(
,
),
将点M中的k换成-
,得到点N(
,
),
(i)当k≠±1时,kMN=
=
=
,
此时直线MN的方程为y=
=
(x-
),
则直线MN过定点(
,0);
(ii)当k=±1时,直线MN的方程为x=
,过点(
,0).
②当弦AB或弦CD的斜率不存在时,直线MN为x轴,过点(
,0),
综上知直线MN必过定点E(
,0).
(2)由(1)知S△FMN=
|EF|•|yM-yN|
=
|
-
|
=
,
设k>0,则S′=
=
,
∴由S′=0,得k=1,又k∈(0,1)时,S′>0,k∈(1,+∞)时,S′<0,
∴当k=1时,S有最大值
,
∴△FMN的面积的最大值为
.
①当弦AB,CD的斜率均存在时,设AB的斜率为k,则CD的斜率为-
| 1 |
| k |
设AB:y=k(x-1),代入椭圆
| x2 |
| 3 |
| y2 |
| 2 |
得(3k2+2)x2-6k2x+(3k2-6)=0,
∴xM=
| xA+xB |
| 2 |
| 3k2 |
| 3k2+2 |
| -2k |
| 3k2+2 |
∴M(
| 3k2 |
| 3k2+2 |
| -2k |
| 3k2+2 |
将点M中的k换成-
| 1 |
| k |
| 3 |
| 2k2+3 |
| 2k |
| 2k2+3 |
(i)当k≠±1时,kMN=
| ||||
| 3-3k2 |
| 10k(k2+1) |
| 6-6k4 |
| -5k |
| 3k2-3 |
此时直线MN的方程为y=
| 2k |
| 2k2+3 |
| -5k |
| 3k2-3 |
| 3 |
| 2k2+3 |
则直线MN过定点(
| 3 |
| 5 |
(ii)当k=±1时,直线MN的方程为x=
| 3 |
| 5 |
| 3 |
| 5 |
②当弦AB或弦CD的斜率不存在时,直线MN为x轴,过点(
| 3 |
| 5 |
综上知直线MN必过定点E(
| 3 |
| 5 |
(2)由(1)知S△FMN=
| 1 |
| 2 |
=
| 1 |
| 5 |
| -2k |
| 3k2+2 |
| 2k |
| 2k2+3 |
=
| |2k(k21)| |
| (3k2+2)(2k2+3) |
设k>0,则S′=
| -12k6-10k4+10k2+12 |
| (3k2+2)2(2k2+3)2 |
=
| (-12k4+2k2-12)(k2-1) |
| (3k2+2)2(2k2+3)2 |
∴由S′=0,得k=1,又k∈(0,1)时,S′>0,k∈(1,+∞)时,S′<0,
∴当k=1时,S有最大值
| 4 |
| 25 |
∴△FMN的面积的最大值为
| 4 |
| 25 |
点评:本题考查直线过定点的证明,考查定点坐标的求法,考查三角形面积的最大值的求法,解题时要注意导数性质的合理运用.

练习册系列答案
相关题目
已知an=2,amn=16,则m的值为( )
| A、3 |
| B、4 |
| C、a3 |
| D、a6 |
 已知椭圆C1:
已知椭圆C1: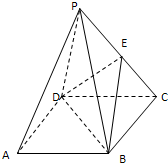 ,底面BCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
,底面BCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.