题目内容
函数f(x)=(x2-1)
的零点个数是( )
| x2-4 |
| A、1 | B、2 | C、3 | D、4 |
考点:函数的零点
专题:函数的性质及应用
分析:先求函数的定义域,然后解方程f(x)=0,即可解得函数零点的个数.
解答:
解:要使函数有意义,则x2-4≥0,
即x2≥4,x≥2或x≤-2.
由f(x)=0得x2-4=0或x2-1=0(不成立舍去).
即x=2或x=-2,
∴函数的零点个数为2个.
故选:B.
即x2≥4,x≥2或x≤-2.
由f(x)=0得x2-4=0或x2-1=0(不成立舍去).
即x=2或x=-2,
∴函数的零点个数为2个.
故选:B.
点评:本题主要考查函数零点的求法和判断,先求函数的定义域是解决本题的关键,否则容易出错.

练习册系列答案
相关题目
已知x,y满足(x-1)2+y2=16,则x2+y2的最小值为( )
| A、3 | B、5 | C、9 | D、25 |
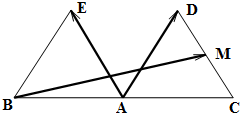 如图,△ABE与△ACD都是正三角形,且
如图,△ABE与△ACD都是正三角形,且| BA |
| AC |
| CM |
| MD |
| BM |
| AE |
| AD |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
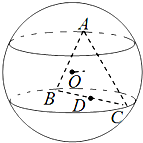 正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为
正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为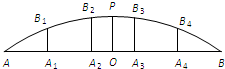 圆拱桥的一孔圆拱如图所示,该圆拱是一段圆弧,其跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一根支柱支撑.
圆拱桥的一孔圆拱如图所示,该圆拱是一段圆弧,其跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一根支柱支撑.