题目内容
函数f(x)=
+2sinx.
(Ⅰ)在△ABC中,cosA=-
,求f(A)的值;
(Ⅱ)求函数f(x)的最小正周期及其图象的所有对称轴的方程.
| cos2x |
| sinx+cosx |
(Ⅰ)在△ABC中,cosA=-
| 3 |
| 5 |
(Ⅱ)求函数f(x)的最小正周期及其图象的所有对称轴的方程.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:计算题
分析:(Ⅰ)利用2倍角的余弦公式与平方差公式,把函数解析式化简为f(x)=cosx+sinx=
sin(x+
),再利用A的范围求出sinA,可求f(A);
(Ⅱ)根据函数解析式可得f(x)的最小正周期T=2π.令x+
=kπ+
,k∈Z,求出x=kπ+
,k∈Z,即为对称轴方程.
| 2 |
| π |
| 4 |
(Ⅱ)根据函数解析式可得f(x)的最小正周期T=2π.令x+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
解答:
解:(Ⅰ)由sinx+cosx≠0得x≠kπ-
,k∈Z.
f(x)=
+2sinx=
+2sinx=cosx+sinx=
sin(x+
),
因为在△ABC中,cosA=-
<0,
所以
<A<π,
所以sinA=
=
,
所以f(A)=sinA+cosA=
-
=
.
(Ⅱ)由(Ⅰ)可得f(x)=
sin(x+
),
所以f(x)的最小正周期T=2π.
因为函数y=sinx的对称轴为x=kπ+
,k∈Z,
又由x+
=kπ+
,k∈Z,得x=kπ+
,k∈Z,
所以f(x)的对称轴的方程为x=kπ+
,k∈Z.
| π |
| 4 |
f(x)=
| cos2x |
| sinx+cosx |
| cos2x-sin2x |
| sinx+cosx |
| 2 |
| π |
| 4 |
因为在△ABC中,cosA=-
| 3 |
| 5 |
所以
| π |
| 2 |
所以sinA=
| 1-cos2A |
| 4 |
| 5 |
所以f(A)=sinA+cosA=
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
(Ⅱ)由(Ⅰ)可得f(x)=
| 2 |
| π |
| 4 |
所以f(x)的最小正周期T=2π.
因为函数y=sinx的对称轴为x=kπ+
| π |
| 2 |
又由x+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
所以f(x)的对称轴的方程为x=kπ+
| π |
| 4 |
点评:本题考查了2倍角的余弦公式,两角和的正弦公式及平方差公式,考查了三角函数的最小正周期的求法及对称轴方程,解题的关键是对三角函数式的化简.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
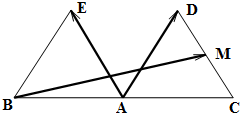 如图,△ABE与△ACD都是正三角形,且
如图,△ABE与△ACD都是正三角形,且| BA |
| AC |
| CM |
| MD |
| BM |
| AE |
| AD |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
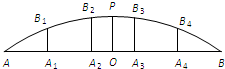 圆拱桥的一孔圆拱如图所示,该圆拱是一段圆弧,其跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一根支柱支撑.
圆拱桥的一孔圆拱如图所示,该圆拱是一段圆弧,其跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一根支柱支撑.