Question

若实数x，y满足0＜x≤2，0＜y≤2，且使关于t的方程t²+2xt+y=0与t²+2yt+x=0均有实数根，则2x+y有（　　）

• A、最小值2
• B、最小值3
• C、最大值2+2

  2

• D、最大值4+

  2

Answer 1

考点：二次函数的性质,简单线性规划

专题：不等式的解法及应用

分析：作出不等式组对应的平面区域，利用z=2x+y的几何意义，即可求出z=2x+y的最值．

解答： 解：由于实数x，y满足0＜x≤2，0＜y≤2，且使关于t的方程t²+2xt+y=0与t²+2yt+x=0均有实数根，
则

4x2-4y≥0 4y2-4x≥0 0＜x≤2 0＜y≤2

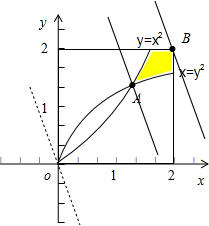
，作出不等式组对应的平面区域如图：
由z=2x+y得y=-2x+z，
平移直线y=-2x，由图象可知，
当直线y=-2x+z经过点A时，y=-2x+z的截距最小，此时z最小．
当直线y=-2x+z经过点B（2，2）时，y=-2x+z的截距最大，此时z最大．
由于

x2=y y2=x

，则A（1，1），
故z=2x+y有最小值3，最大值6．
故选：B．

点评：本题主要考查线性规划的应用，利用2x+y的几何意义结合数形结合，即可求出2x+y的最值．