题目内容
数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为( )
| A、2n-n-1 |
| B、2n+1-n-2 |
| C、2n |
| D、2n+1-n |
考点:数列的求和
专题:等差数列与等比数列
分析:把已知数列的通项利用等比数列的前n项和化简,然后利用分组求和得答案.
解答:
解:∵1+2+22+…+2n-1=
=2n-1,
∴数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和:
Sn=21-1+22-1+…+2n-1=(21+22+…+2n)-n
=
-n=2n+1-n-2.
故选:B.
| 1×(1-2n) |
| 1-2 |
∴数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和:
Sn=21-1+22-1+…+2n-1=(21+22+…+2n)-n
=
| 2×(1-2n) |
| 1-2 |
故选:B.
点评:本题考查了数列的和的求法,考查了等比数列的前n项和公式,是中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
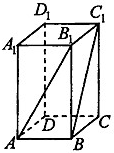 如图,在长方体ABCD-A1B1C1D1中,AB=
如图,在长方体ABCD-A1B1C1D1中,AB=| 2 |
| 3 |
| 6 |
| A、60° | B、45° |
| C、30° | D、15° |
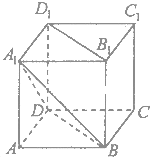 如图,在正方体ABCD-A1B1C1D1中,AB=2.
如图,在正方体ABCD-A1B1C1D1中,AB=2.