题目内容
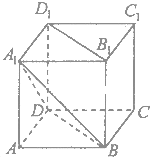 如图,在正方体ABCD-A1B1C1D1中,AB=2.
如图,在正方体ABCD-A1B1C1D1中,AB=2.(Ⅰ)求A1B与B1D1所成角的大小;
(Ⅱ)求三棱锥A-BDA1的体积.
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:空间角
分析:(Ⅰ)连接BD,DA1,容易得到∠DBA1=60°,且BD∥B1D1,所以A1B与B1D1所成的角为60°;
(Ⅱ)通过图形可看出V三棱锥A-BDA1=V三棱锥A1-ABD=
•2•2=
.
(Ⅱ)通过图形可看出V三棱锥A-BDA1=V三棱锥A1-ABD=
| 1 |
| 3 |
| 4 |
| 3 |
解答:
解:(Ⅰ)如图,连接BD,DA1,则B1D1∥BD,且△BA1D为等边三角形;
∴∠DBA1=60°;
即A1B与B1D1所成角的大小为60°;
(Ⅱ)由图可看出三棱锥A-BDA1的体积等于三棱锥A1-ABD的体积;
∵A1A⊥底面ABD,所以三棱锥A1-ABD的高是A1A=2,S底面ABD=2;
∴V三棱锥A1-ABD=
•2•2=
;
∴三棱锥A-BDA1的体积为
.
∴∠DBA1=60°;
即A1B与B1D1所成角的大小为60°;
(Ⅱ)由图可看出三棱锥A-BDA1的体积等于三棱锥A1-ABD的体积;
∵A1A⊥底面ABD,所以三棱锥A1-ABD的高是A1A=2,S底面ABD=2;
∴V三棱锥A1-ABD=
| 1 |
| 3 |
| 4 |
| 3 |
∴三棱锥A-BDA1的体积为
| 4 |
| 3 |
点评:考查异面直线所成角的概念及求法,三棱锥的体积公式.

练习册系列答案
相关题目
若集合A、B、C,满足A∩B=A,B∪C=C,则A与C之间的关系为( )
| A、A?C | B、C?A |
| C、A⊆C | D、C⊆A |
不等式
<0的解集为( )
| x-2 |
| |x|-1 |
| A、{x|1<x<2} |
| B、{x|x<2且x≠1} |
| C、{x|-1<x<2且x≠1} |
| D、{x|x<-1或1<x<2} |
下列命题说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“0<x<3”是“|x-1|<1”的必要不充分条件 |
| C、命题“?x∈R,使得x2+x-1<0”的否定是:“?x∈R,均有x2+x-1>0” |
| D、命题“若x=y,则sinx=siny”的逆命题为真命题 |
数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为( )
| A、2n-n-1 |
| B、2n+1-n-2 |
| C、2n |
| D、2n+1-n |