题目内容

17．已知函数f（x）=x3+3x2-9x-3
（Ⅰ）若函数f（x）在点（x0，f（x0））处的切线l与直线x-9y+1=0垂直，求切线l的方程；
（Ⅱ）求函数f（x）的极值．

分析 （Ⅰ）求出导函数，求出斜率，利用直线的垂直关系求解切线方程即可．
（Ⅱ）求出导函数，判断函数的单调性，然后求解函数的极值．

解答 解：（Ⅰ）f'（x）=3x2+6x-9
根据题意得$f'（{x_0}）=3{x_0}^2+6{x_0}-9=-9$；∴x0=0或-2；
∴①当x0=0时，f（x0）=-3；∴切线方程为y=-9x-3；
②当x0=-2时，f（x0）=19；切线方程为y=-9x+1； 
综上切线l方程为9x+y+3=0或  9x+y-1=0…（6分）
（Ⅱ）f'（x）=3（x+3）（x-1）；
令f'（x）＞0，则x＞1或x＜-3，令f'（x）＜0，则-3＜x＜1
∴f（x）的极大值为f（-3）=24，f（x）的极小值为f（1）=-8．…（12分）

点评 本题考查函数的极值的求法，切线方程以及函数的单调性的应用，考查计算能力．

练习册系列答案
相关题目
7．已知椭圆C的一个顶点为A（0，-1），焦点在x轴上，其右焦点到直线$x-y+2\sqrt{2}=0$的距离为3．
（1）求椭圆C的方程；
（2）设直线l：y=x+m，是否存在实数m，使直线l与椭圆C有两个不同的交点M，N，且|AM|=|AN|，若存在，求出m的值；若不存在，请说明理由．
8．在直角坐标系xOy中，圆C1和C2的参数方程分别是$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$（φ为参数）和$\left\{\begin{array}{l}x=cosβ\\ y=1+sinβ\end{array}\right.$（β为参数），以O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系；
（1）求圆C1和C2的极坐标方程；
（2）射线$OM：θ=α（0＜α＜\frac{π}{2}）$与圆C1的交点为O、P，与圆C2的交点为O、Q，求|OP|•|OQ|的最大值．
5．袋中有2个白球和4个黑球，每次从中任取一个球，每次取出的黑球不再放回，直到取出1个白球为止．求取球次数X的概率分布列．
12．执行如图框图，已知输出的s∈[0，4]，若输入的t∈[m，n]，则实数n-m的最大值为（　　
A．1B．2C．3D．4
2．已知直线l的参数方程为$\left\{\begin{array}{l}x=t\\ y=4+t\end{array}\right.$（t为参数），圆C的极坐标方程为$ρ=2\sqrt{2}sin（θ+\frac{π}{4}）$，则圆上的点到直线l的最大距离为$3\sqrt{2}$．
9．在空间直角坐标系中，点$P（1，\sqrt{2}，\sqrt{3}）$，过点P作平面xOy的垂线PQ，则垂足Q的坐标为（1，$\sqrt{2}$，0）．
6．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}x=2+2cosα\\ y=2sinα\end{array}\right.$，参数α∈（0，π），M为C1上的动点，满足条件$\overrightarrow{OM}=2\overrightarrow{OP}$的点P的轨迹为曲线C2．
（Ⅰ）求C2的普通方程；
（Ⅱ）在以O为极点，x轴的非负半轴为极轴的极坐标系中，射线$θ=\frac{π}{3}$与C1，C2分别交于A，B两点，求|AB|．
7．一个几何体的三视图如图所示，则该几何体的体积为（　　）
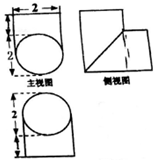
A．4πB．6πC．8πD．16π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网