题目内容
6.在直角坐标系xOy中,曲线C1的参数方程为$\left\{\begin{array}{l}x=2+2cosα\\ y=2sinα\end{array}\right.$,参数α∈(0,π),M为C1上的动点,满足条件$\overrightarrow{OM}=2\overrightarrow{OP}$的点P的轨迹为曲线C2.(Ⅰ)求C2的普通方程;
(Ⅱ)在以O为极点,x轴的非负半轴为极轴的极坐标系中,射线$θ=\frac{π}{3}$与C1,C2分别交于A,B两点,求|AB|.
分析 (I)设P(x,y),则M(2x,2y),代入C1的方程可得$\left\{\begin{array}{l}2x=2+2cosα\\ 2y=2sinα\end{array}\right.$,即$\left\{\begin{array}{l}x=1+cosα\\ y=sinα\end{array}\right.$,α∈(0,π).消去参数可得普通方程所以,C2的普通方程为(x-1)2+y2=1,0<y≤1.
(II)C1的极坐标方程为:$ρ=4cosθ,\;(0<θ<\frac{π}{2})$,C2的极坐标方程为:$ρ=2cosθ,\;(0<θ<\frac{π}{2})$,分别联立解出即可得出.
解答 解:(I)设P(x,y),则M(2x,2y),
因为M为C1上的动点,所以$\left\{\begin{array}{l}2x=2+2cosα\\ 2y=2sinα\end{array}\right.$,即$\left\{\begin{array}{l}x=1+cosα\\ y=sinα\end{array}\right.$,α∈(0,π).
消去参数得(x-1)2+y2=1,0<y≤1.
所以,C2的普通方程为(x-1)2+y2=1,0<y≤1.
(II)C1的极坐标方程为:$ρ=4cosθ,\;(0<θ<\frac{π}{2})$,C2的极坐标方程为:$ρ=2cosθ,\;(0<θ<\frac{π}{2})$,
由$\left\{\begin{array}{l}θ=\frac{π}{3}\\ ρ=4cosθ,\;(0<θ<\frac{π}{2})\end{array}\right.$得点A的极坐标为$(2,\;\frac{π}{3})$,
由$\left\{\begin{array}{l}θ=\frac{π}{3}\\ ρ=2cosθ,\;(0<θ<\frac{π}{2})\end{array}\right.$得点B的极坐标为$(1,\;\frac{π}{3})$,
所以,|AB|=1.
点评 本题考查了极坐标方程的应用、参数方程化为普通方程、切线交点,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |
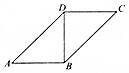 如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.
如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.