题目内容
7.一个几何体的三视图如图所示,则该几何体的体积为( )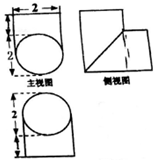
| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
分析 由题意,直观图是两个垂直相交的圆柱组合体,
其体积等于以1为半径的圆为底,3+1为高的圆柱的体积,即可得出结论.
解答 解:由题意,直观图是两个垂直相交的圆柱组合体,
其体积等于以1为半径的圆为底,3+1为高的圆柱的体积,即π•12•4=4π,
故选A.
点评 本题考查的知识点是由三视图,求体积,根据已知的三视图,判断几何体的形状是解答的关键.
注意:三视图中的尺寸是“长对正,高平齐,宽相等.属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.我国古代数学著作《九章算术》有如下问题:“今有金杖,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”其大意是:“现有一根长五尺的金杖,一头粗,一头细.在粗的一端截下1尺重4斤.在细的一端截下1尺,重2斤.问依次每一尺各重多少斤?”根据上面的已知条件,若金杖由粗到细是均匀变化的,则金杖的质量为( )
| A. | 12斤 | B. | 15斤 | C. | 15.5斤 | D. | 18斤 |
2.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,若对任意给定的y∈(2,+∞),都存在唯一的x∈R,满足f(f(x))=2a2y2+ay,则正实数a的最小值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
19.设Sn为等比数列{an}的前n项和,a3=8a6,则$\frac{S_4}{S_2}$的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | 5 |
17.设全集U=R,集合A={x|x2-2x-3<0},B={x|x-1≥0},则图中阴影部分所表示的集合为( )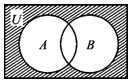

| A. | {x|x≤-1或x≥3} | B. | {x|x<1或x≥3} | C. | {x|x≤1} | D. | {x|x≤-1} |
