题目内容
5.袋中有2个白球和4个黑球,每次从中任取一个球,每次取出的黑球不再放回,直到取出1个白球为止.求取球次数X的概率分布列.分析 由题意知X的所有可能取值为1,2,3,4,5,计算对应的概率值即可.
解答 解:由题意知X的所有可能取值为:1,2,3,4,5;
则P(X=1)=$\frac{{C}_{2}^{1}}{{C}_{6}^{1}}$=$\frac{1}{3}$,
P(X=2)=$\frac{{C}_{4}^{1}{•C}_{2}^{1}}{{A}_{6}^{2}}$=$\frac{4}{15}$,
P(X=3)=$\frac{{C}_{4}^{1}{•C}_{3}^{1}{•C}_{2}^{1}}{{A}_{6}^{3}}$=$\frac{1}{5}$,
P(X=4)=$\frac{{C}_{4}^{1}{•C}_{3}^{1}{•C}_{2}^{1}{•C}_{2}^{1}}{{A}_{6}^{4}}$=$\frac{2}{15}$,
P(X=5)=$\frac{{C}_{4}^{1}{•C}_{3}^{1}{•C}_{2}^{1}{•C}_{1}^{1}{•C}_{2}^{1}}{{A}_{6}^{5}}$=$\frac{1}{15}$;
∴取球次数X的概率分布列为:
| X | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{3}$ | $\frac{4}{15}$ | $\frac{1}{5}$ | $\frac{2}{15}$ | $\frac{1}{15}$ |
点评 本题考查了离散型随机变量的分布列问题,是基础题.

练习册系列答案
相关题目
15.若实数x,y满足不等式$\left\{\begin{array}{l}x+3y-3≥0\\ 2x-y-3≥0\\ x-my+1≥0\end{array}\right.$,且x+y的最大值为9,则实数m=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
16.设全集U=R,A={x|-2<x<1},B={x|2x>1},则A∩(∁UB)=( )
| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |
20.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若$\overrightarrow{AB}=\vec a$,$\overrightarrow{BC}=\vec b$,$\overrightarrow{A{A_1}}=\vec c$,则$\overrightarrow{BM}$可表示为( )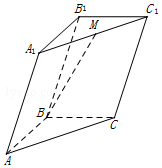

| A. | $-\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | C. | $-\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ | D. | $\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ |
 沿一个正方体三个面的对角线截得的几何体如图所示,若正视图的视线方向与前面的三角形面垂直,则该几何体的左视图为( )
沿一个正方体三个面的对角线截得的几何体如图所示,若正视图的视线方向与前面的三角形面垂直,则该几何体的左视图为( )



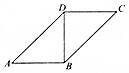 如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.
如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.