题目内容
7.已知椭圆C的一个顶点为A(0,-1),焦点在x轴上,其右焦点到直线$x-y+2\sqrt{2}=0$的距离为3.(1)求椭圆C的方程;
(2)设直线l:y=x+m,是否存在实数m,使直线l与椭圆C有两个不同的交点M,N,且|AM|=|AN|,若存在,求出m的值;若不存在,请说明理由.
分析 (1)利用椭圆的性质得到c,求出a,b,即可求解椭圆方程.
(2)设M(x1,y1)N(x2,y2),联立直线与椭圆方程,利用判别式以及韦达定理,求出MN的中点坐标,利用AM=AN,验证m是否存在即可.
解答 解:(1)因为焦点在x轴,顶点A(0,-1),∴b=1,设右焦点坐标为(c,0),
由题意得$\frac{{|{c+2\sqrt{2}}|}}{{\sqrt{2}}}=3$,∴$c=\sqrt{2}$,
可得b=1,
∴$\frac{x^2}{3}+\frac{y^2}{1}=1$;
(2)设M(x1,y1)N(x2,y2),$\left\{{\begin{array}{l}{y=x+m}\\{{x^2}+3{y^2}-3=0}\end{array},4{x^2}+6mx+3{m^2}-3=0,\left\{{\begin{array}{l}{△=36{m^2}-16({3{m^2}-3})>0}\\{{x_1}+{x_2}=-\frac{3m}{2}}\end{array}}\right.}\right.$,
即M,N的中点坐标$Q({-\frac{3m}{4},\frac{m}{4}})$,∵AM=AN,
∴kAQ=-1,∴m=2经检验△=0不合题意,
∴不存在.
点评 本题考查直线与椭圆的位置关系的综合应用,椭圆方程的求法,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知函数f(x)的定义域为[-2,2],且f(x)在[-2,2]上是增函数,f(1-m)<f(m),则实数m的取值范围为( )
| A. | $(\frac{1}{2},+∞)$ | B. | $(-∞,\frac{1}{2})$ | C. | $({\frac{1}{2},2}]$ | D. | $[{-2,\frac{1}{2}})$ |
15.若实数x,y满足不等式$\left\{\begin{array}{l}x+3y-3≥0\\ 2x-y-3≥0\\ x-my+1≥0\end{array}\right.$,且x+y的最大值为9,则实数m=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
2.如图是某四棱锥的三视图,则该几何体的表面积等于( )
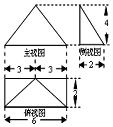

| A. | 34+6$\sqrt{5}$ | B. | 44+12$\sqrt{5}$ | C. | 34+6$\sqrt{3}$ | D. | 32+6$\sqrt{5}$ |
16.设全集U=R,A={x|-2<x<1},B={x|2x>1},则A∩(∁UB)=( )
| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |