题目内容
9.在空间直角坐标系中,点$P(1,\sqrt{2},\sqrt{3})$,过点P作平面xOy的垂线PQ,则垂足Q的坐标为(1,$\sqrt{2}$,0).分析 根据题意画出图形,结合图形,即可求出点Q的坐标.
解答 解:空间直角坐标系中,点$P(1,\sqrt{2},\sqrt{3})$,过点P作平面xOy的垂线PQ,
垂足为Q,则点Q的坐标为(1,$\sqrt{2}$,0);
如图所示.
故答案为:$(1,\sqrt{2},0)$.
点评 本题考查了空间直角坐标系的应用问题,是基础题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
20.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若$\overrightarrow{AB}=\vec a$,$\overrightarrow{BC}=\vec b$,$\overrightarrow{A{A_1}}=\vec c$,则$\overrightarrow{BM}$可表示为( )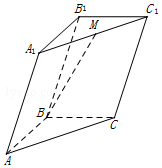

| A. | $-\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | C. | $-\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ | D. | $\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ |
4.已知α,β,γ是三个不同的平面,l1,l2是两条不同的直线,下列命题是真命题的是( )
| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若l1∥α,l1⊥β,则α∥β | ||
| C. | 若α∥β,l1∥α,l2∥β,则l1∥l2 | D. | 若α⊥β,l1⊥α,l2⊥β,则l1⊥l2 |
18.我国古代数学著作《九章算术》有如下问题:“今有金杖,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”其大意是:“现有一根长五尺的金杖,一头粗,一头细.在粗的一端截下1尺重4斤.在细的一端截下1尺,重2斤.问依次每一尺各重多少斤?”根据上面的已知条件,若金杖由粗到细是均匀变化的,则金杖的质量为( )
| A. | 12斤 | B. | 15斤 | C. | 15.5斤 | D. | 18斤 |
19.设Sn为等比数列{an}的前n项和,a3=8a6,则$\frac{S_4}{S_2}$的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | 5 |
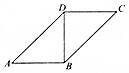 如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.
如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.