题目内容
 如图,△ABC中,延长CB到D,使BD=BC,当E点在线段AD上移动时,若
如图,△ABC中,延长CB到D,使BD=BC,当E点在线段AD上移动时,若| AE |
| AB |
| AC |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:
,
共线,所以存在实数k使
=k
,0≤k≤1,根据向量的加法和减法以及B是CD中点,可用
,
表示
为:
=2
-
,所以又可以用
,
表示
为:
=2k
-k
=λ
+μ
,所以根据平面向量基本定理得:
,λ-μ=3k≤3,所以最大值是3.
| AE |
| AD |
| AE |
| AD |
| AB |
| AC |
| AD |
| AD |
| AB |
| AC |
| AB |
| AC |
| AE |
| AE |
| AB |
| AC |
| AB |
| AC |
|
解答:
解:设
=k
=k(
+2
)=k[
+2(
-
)]=2k
-k
,0≤k≤1;
又
=λ
+μ
;
∴
;
∴t=λ-μ=3k,0≤k≤1;
∴k=1时t取最大值3.
即t=λ-μ的最大值为3.
故答案为:3.
| AE |
| AD |
| AC |
| CB |
| AC |
| AB |
| AC |
| AB |
| AC |
又
| AE |
| AB |
| AC |
∴
|
∴t=λ-μ=3k,0≤k≤1;
∴k=1时t取最大值3.
即t=λ-μ的最大值为3.
故答案为:3.
点评:考查共线向量基本定理,向量的加法、减法运算,以及平面向量基本定理.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
设α∈(0,
),β∈(0,
),且tanα=
,则下列结论中正确的是( )
| π |
| 2 |
| π |
| 4 |
| 1+sin2β |
| cos2β |
A、2α-β=
| ||
B、2α+β=
| ||
C、α-β=
| ||
D、α+β=
|
已知实数a,b,c满足
,则a+b的取值范围是( )
|
A、(
| ||||
B、(1,
| ||||
C、(1,
| ||||
D、(-
|
点A、B、C、D在同一个球的球面上,AB=BC=AC=
,若四面体ABCD体积的最大值为
,则这个球的表面积为( )
| 3 |
| 3 |
A、
| ||
| B、8π | ||
C、
| ||
D、
|
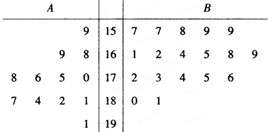 某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.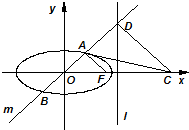 已知椭圆Γ:
已知椭圆Γ: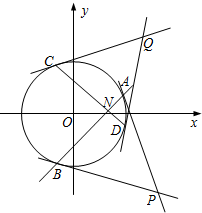 已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.
已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.