题目内容
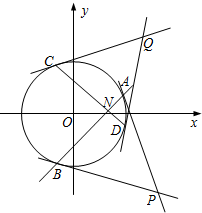 已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.
已知直线l:y=x-1与⊙O:x2+y2=4相交于A,B两点,过点A,B的两条切线相交于点P.(1)求点P的坐标;
(2)若N为线段AB上的任意一点(不包括端点),过点N的直线交⊙O于C,D两点,过点C、D的两条切线相交于点Q,判断点Q的轨迹是否经过定点?若过定点,求出该点的坐标;若不过定点,说明理由.
考点:直线和圆的方程的应用
专题:计算题,综合题,圆锥曲线的定义、性质与方程
分析:(1)设P(x1,y1),则过点O,A,B,P的圆的方程为x(x-x1)+y(y-y1)=0,与x2+y2=4联立可得x1x+y1y=4,与直线直线l:y=x-1重合,故可得点P的坐标;
(2)设N(x0,y0),Q(x2,y2)可得x2x0+y2y0=4,y0=x0-1,则点Q的轨迹为动直线x0x+(x0-1)y=4,则恒成立可得
,从而解得.
(2)设N(x0,y0),Q(x2,y2)可得x2x0+y2y0=4,y0=x0-1,则点Q的轨迹为动直线x0x+(x0-1)y=4,则恒成立可得
|
解答:
解:(1)设P(x1,y1),
则过点O,A,B,P的圆的方程为x(x-x1)+y(y-y1)=0.
即x2+y2-x1x-y1y=0…①
又因为⊙O:x2+y2=4…②
由①-②得,x1x+y1y=4,即为直线AB的方程.
又因为AB方程为y=x-1,
所以
=
=
,解得x1=4,y1=-4,
所以点P的坐标为(4,-4).
(2)设N(x0,y0),Q(x2,y2),
由(1)可知直线CD的方程为:x2x+y2y=4,
因为N(x0,y0)在直线CD上,所以x2x0+y2y0=4.
又因为N(x0,y0)在直线AB上,所以y0=x0-1.
即x2x0+y2(x0-1)=4,
所以点Q的轨迹为动直线x0x+(x0-1)y=4.
如果点Q的轨迹过定点,那么x0x+(x0-1)y=4与x0无关.
即(x+y)x0-y-4=0与x0无关,
所以
解得
所以点Q的轨迹恒过定点(4,-4).
则过点O,A,B,P的圆的方程为x(x-x1)+y(y-y1)=0.
即x2+y2-x1x-y1y=0…①
又因为⊙O:x2+y2=4…②
由①-②得,x1x+y1y=4,即为直线AB的方程.
又因为AB方程为y=x-1,
所以
| x1 |
| -1 |
| y1 |
| -1 |
| 4 |
| -1 |
所以点P的坐标为(4,-4).
(2)设N(x0,y0),Q(x2,y2),
由(1)可知直线CD的方程为:x2x+y2y=4,
因为N(x0,y0)在直线CD上,所以x2x0+y2y0=4.
又因为N(x0,y0)在直线AB上,所以y0=x0-1.
即x2x0+y2(x0-1)=4,
所以点Q的轨迹为动直线x0x+(x0-1)y=4.
如果点Q的轨迹过定点,那么x0x+(x0-1)y=4与x0无关.
即(x+y)x0-y-4=0与x0无关,
所以
|
|
所以点Q的轨迹恒过定点(4,-4).
点评:本题考查了圆锥曲线与直线的位置关系及恒成立问题的处理方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=(
)x-
的图象可能是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、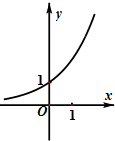 |
B、 |
C、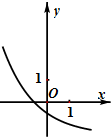 |
D、 |
 如图,△ABC中,延长CB到D,使BD=BC,当E点在线段AD上移动时,若
如图,△ABC中,延长CB到D,使BD=BC,当E点在线段AD上移动时,若 已知函数f(x)=
已知函数f(x)=