题目内容
点A、B、C、D在同一个球的球面上，AB=BC=AC=
，若四面体ABCD体积的最大值为
，则这个球的表面积为（ ）
| 3 |
| 3 |
A、
| ||
| B、8π | ||
C、
| ||
D、
|
考点：球的体积和表面积
专题：综合题,空间位置关系与距离
分析：根据几何体的特征，判定外接球的球心，求出球的半径，即可求出球的表面积．
解答：
解：根据题意知，△ABC是一个等边三角形，其面积为
，外接圆的半径为1．
小圆的圆心为Q，若四面体ABCD的体积的最大值，由于底面积S△ABC不变，高最大时体积最大，
所以，DQ与面ABC垂直时体积最大，最大值为
S△ABC×DQ=
，
∴DQ=4，
设球心为O，半径为R，
则在直角△AQO中，OA2=AQ2+OQ2，即R2=12+（4-R）2，∴R=
则这个球的表面积为：S=4π（
）2=
故选C．
3
| ||
| 4 |
小圆的圆心为Q，若四面体ABCD的体积的最大值，由于底面积S△ABC不变，高最大时体积最大，
所以，DQ与面ABC垂直时体积最大，最大值为
| 1 |
| 3 |
| 3 |
∴DQ=4，
设球心为O，半径为R，
则在直角△AQO中，OA2=AQ2+OQ2，即R2=12+（4-R）2，∴R=
| 17 |
| 8 |
则这个球的表面积为：S=4π（
| 17 |
| 8 |
| 289π |
| 16 |
故选C．
点评：本题考查的知识点是球内接多面体，球的表面积，其中分析出何时四面体ABCD的体积的最大值，是解答的关键．
练习册系列答案
相关题目
如图，△ABC中，延长CB到D，使BD=BC，当E点在线段AD上移动时，若函数y=(
)x-
的图象可能是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
A、 |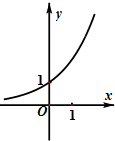
B、 |
C、 |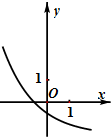
D、 |
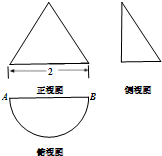一个几何体的三视图如图所示，其中正视图是等边三角形，俯视图是半圆．现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点，则蚂蚁所经过路程的最小值为