题目内容
设α∈(0，
)，β∈(0，
)，且tanα=
，则下列结论中正确的是（ ）
| π |
| 2 |
| π |
| 4 |
| 1+sin2β |
| cos2β |
A、2α-β=
| ||
B、2α+β=
| ||
C、α-β=
| ||
D、α+β=
|
考点：二倍角的余弦,二倍角的正弦
专题：三角函数的求值
分析：利用二倍角公式得出
，然后分子分母同时除以cosβ，最后由角的范围得出答案即可．
| sinβ+cosβ |
| cosβ-sinβ |
解答：
解：tanα=
=
=
=
=tan(β+
)．
因为α∈(0，
)，β+
∈（
，
），所以α=β+
．
故选：C．
| 1+sin2β |
| cos2β |
| (sinβ+cosβ)2 |
| cos2β-sin2β |
| sinβ+cosβ |
| cosβ-sinβ |
| 1+tanβ |
| 1-tanβ |
| π |
| 4 |
因为α∈(0，
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
故选：C．
点评：本题主要考查了二倍角的应用，属于基础题．
练习册系列答案
相关题目
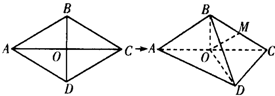如图，平面四边形ABCD中，AB=BC=CD=DA=BD=6，O为AC，BD的交点．将四边形ABCD沿对角线AC折起，得到三棱锥B-ACD，且BD=3
如图，△ABC中，延长CB到D，使BD=BC，当E点在线段AD上移动时，若