题目内容
16.设△ABC的内角A,B,C所对边的长分别为a,b,c,若$\frac{b}{c}$=$\frac{1}{2}$,B=2C,a=4,则b的值为( )| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\frac{8}{3}$ | D. | 2 |
分析 B=2C,利用倍角公式可得:sinB=sin2C=2sinCcosC,由b=2ccosC,又$\frac{b}{c}$=$\frac{1}{2}$,可得cosC=$\frac{1}{4}$.再利用余弦定理即可得出.
解答 解:B=2C,∴sinB=sin2C=2sinCcosC,
∴b=2ccosC,又$\frac{b}{c}$=$\frac{1}{2}$,
∴cosC=$\frac{1}{4}$.
∴$\frac{1}{4}$=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,∴$\frac{1}{4}$=$\frac{16+{b}^{2}-4{b}^{2}}{8b}$,解得b=2.
故选:D.
点评 本题考查了正弦定理余弦定理、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
6.$\sqrt{1+sin6}$+$\sqrt{1-sin6}$=( )
| A. | 2sin3 | B. | -2sin3 | C. | 2cos3 | D. | -2cos3 |
7.一个几何体的三视图及其尺寸如图所示,则该几何体的表面积为( )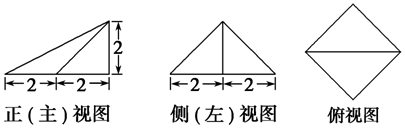

| A. | 2$\sqrt{2}$+2$\sqrt{6}$+8 | B. | 4$\sqrt{2}$+4$\sqrt{6}$+8 | C. | 8$\sqrt{2}$+8 | D. | 16 |
8.已知m,n是两条互相垂直的直线,α是平面,则n∥α是m⊥α的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
8.下列四个数中最大的是( )
| A. | (ln2)2 | B. | ln(ln2) | C. | ln$\sqrt{2}$ | D. | ln2 |
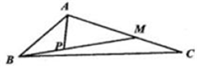 如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.
如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.