题目内容
7.一个几何体的三视图及其尺寸如图所示,则该几何体的表面积为( )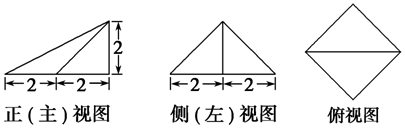
| A. | 2$\sqrt{2}$+2$\sqrt{6}$+8 | B. | 4$\sqrt{2}$+4$\sqrt{6}$+8 | C. | 8$\sqrt{2}$+8 | D. | 16 |
分析 根据几何体的三视图,得出该几何体是底面为菱形,且侧棱垂直于底面的四棱锥,结合图中数据求出该几何体的表面积.
解答 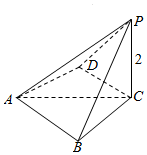 解:根据几何体的三视图,得该几何体是如图所示四棱锥,且四棱锥的底面是菱形,侧棱PC⊥底面ABCD,
解:根据几何体的三视图,得该几何体是如图所示四棱锥,且四棱锥的底面是菱形,侧棱PC⊥底面ABCD,
则该几何体的各侧面中最大的侧面是△PAB与△PAD,其面积相等;
△PAB中,PA=$\sqrt{4+16}$=2$\sqrt{5}$,AB=2$\sqrt{2}$,PB=$\sqrt{4+8}$=2$\sqrt{3}$;
PA2=AB2+PB2,∴△PAB为直角三角形;
∴S△PAB=$\frac{1}{2}$×PB×AB=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{3}$=2$\sqrt{6}$.
S△PCD=S△PCB=$\frac{1}{2}×2×2\sqrt{2}$=2$\sqrt{2}$,SABCD=$2\sqrt{2}×2\sqrt{2}$=8,
∴该几何体的表面积为4$\sqrt{2}$+4$\sqrt{6}$+8,
故选:B.
点评 本题考查了空间三视图的应用问题,考查该几何体的表面积,解题时应根据三视图还原出几何体的结构特征,是基础题目.

练习册系列答案
相关题目
17.若$sinθ=\frac{3}{5}$,且θ是第二象限角,则cosθ=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
18.已知tanα=2,α∈(0,π),则cos($\frac{9π}{2}$+2α)等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{5}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{4}{5}$ |
15.下列函数中最小正周期为π且为偶函数的是( )
| A. | $y=cos(2x-\frac{π}{2})$ | B. | $y=sin(2x+\frac{π}{2})$ | C. | $y=sin(x+\frac{π}{2})$ | D. | $y=cos(x-\frac{π}{2})$ |
12.设集合A={x|x2-1<0},B={y|y=2x,x∈A},则A∩B=( )
| A. | (0,1) | B. | (-1,2) | C. | (-1,+∞) | D. | $(\frac{1}{2},1)$ |
16.设△ABC的内角A,B,C所对边的长分别为a,b,c,若$\frac{b}{c}$=$\frac{1}{2}$,B=2C,a=4,则b的值为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\frac{8}{3}$ | D. | 2 |
20.执行如图所示的程序框图,如果输入a=6,b=2,则输出的S=( )


| A. | 30 | B. | 120 | C. | 360 | D. | 720 |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点.