题目内容
11.某家具厂有方木料90m3,五合板600m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1m3、五合板2m2;生产每个书橱需要方木料0.2m3、五合板1m2.出售一张书桌可获利润80元,出售一个书橱可获利润120元,怎样安排生产可使所得利润最大?最大利润为多少?分析 本题一线性规划的问题,据题意建立起约束条件与目标函数,作出可行域,利用图形求解.
解答 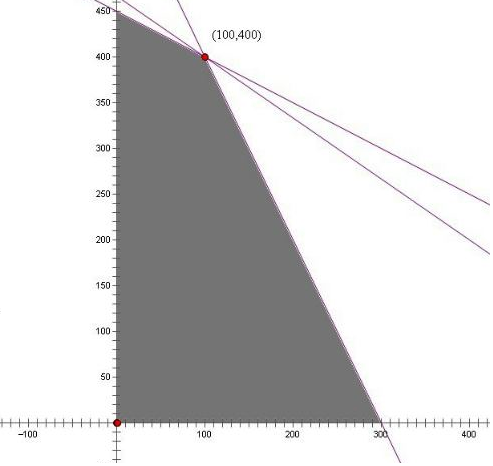 解:设生产书桌x张,书橱y张,利润z元,则目标函数z=80x+120y,
解:设生产书桌x张,书橱y张,利润z元,则目标函数z=80x+120y,
约束条件为$\left\{\begin{array}{l}{0.1x+0.2y≤90}\\{2x+y≤600}\\{x∈N}\\{y∈N}\end{array}\right.$
作出上可行域:
作出一组平行直线2x+3y=t,此直线经过点A(100,400)时,即合理安排生产,生产书桌100张,书橱400个,有最大利润为zmax=80×100+400×120=56000元.
点评 本题考查了性规划的问题,将应用题转化为线性约束条件,再作出其图形,从图形上找出目标函数取最大值的点.算出最优解.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
1.已知点A(-1,-2),B(1,-1),C(x,2),若A、B、C三点共线,则x的值为( )
| A. | -4 | B. | -3 | C. | 2 | D. | 7 |
16.设△ABC的内角A,B,C所对边的长分别为a,b,c,若$\frac{b}{c}$=$\frac{1}{2}$,B=2C,a=4,则b的值为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\frac{8}{3}$ | D. | 2 |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点. 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.