题目内容
9.△ABC中,角A,B,C所对的边分别为a,b,c,且${a^2}+{b^2}+\sqrt{2}ab={c^2}$,则tanAtan2B的取值范围是$(0,\frac{1}{2})$.分析 由且${a^2}+{b^2}+\sqrt{2}ab={c^2}$,可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$-\frac{\sqrt{2}}{2}$,C∈(0,π),解得C=$\frac{3π}{4}$.可得tanAtan2B=tan$(\frac{π}{4}-B)$•tan2B=$\frac{2tanB}{(1+tanB)^{2}}$,再利用基本不等式的性质即可得出.
解答 解:由且${a^2}+{b^2}+\sqrt{2}ab={c^2}$,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$-\frac{\sqrt{2}}{2}$,C∈(0,π),
解得C=$\frac{3π}{4}$.
则tanAtan2B=tan$(\frac{π}{4}-B)$•tan2B=$\frac{1-tanB}{1+tanB}$×$\frac{2tanB}{1-ta{n}^{2}B}$=$\frac{2tanB}{(1+tanB)^{2}}$,
令tanB=t∈(0,1),则$\frac{2t}{1+2t+{t}^{2}}$≤$\frac{2t}{4t}$=$\frac{1}{2}$,等号不成立.
∴$\frac{2tanB}{(1+tanB)^{2}}$∈(0,$\frac{1}{2}$),
故答案为:$(0,\frac{1}{2})$.
点评 本题考查了余弦定理、和差公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.设△ABC的内角A,B,C所对边的长分别为a,b,c,若$\frac{b}{c}$=$\frac{1}{2}$,B=2C,a=4,则b的值为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\frac{8}{3}$ | D. | 2 |
20.执行如图所示的程序框图,如果输入a=6,b=2,则输出的S=( )


| A. | 30 | B. | 120 | C. | 360 | D. | 720 |
17.等比数列{an}的前n项和为Sn,若S14=3S7=3,则S28=( )
| A. | 9 | B. | 15 | C. | 8 | D. | 12 |
19.执行如图的程序框图,如果输入的t=0.01,则输出的n=( )


| A. | 5 | B. | 7 | C. | 10 | D. | 12 |
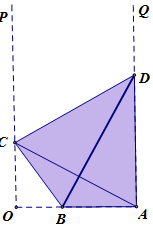 在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,
在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,