题目内容
在△ABC中,E,F分别为AB,AC中点,P为线段EF上任意一点,实数x,y满足
+x
+y
=
,设△ABC,△PCA,△PAB的面积分别为S,S1,S2,记
=λ1,
=λ2,则λ1•λ2取得最大值时,2x+3y的值为 .
| PA |
| PB |
| PC |
| 0 |
| S1 |
| S |
| S2 |
| S |
考点:向量加减混合运算及其几何意义
专题:平面向量及应用
分析: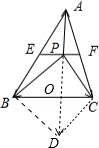 如图所示.由于点P在△ABC的中位线EF上,可得
如图所示.由于点P在△ABC的中位线EF上,可得
=
.于是
=
,即S1+S2=
S.利用基本不等式可得:当且仅当S1=S2=
S时S1S2取得最大值
S2.此时点P为线段EF的中点.以PB、PC为邻边作平行四边形PBDC,连接PD交BC于点O.利用向量的平行四边形法则即可得出x,y的值.
 如图所示.由于点P在△ABC的中位线EF上,可得
如图所示.由于点P在△ABC的中位线EF上,可得| S△BPC |
| S |
| 1 |
| 2 |
| S1+S2 |
| S |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
解答:
解:如图所示.
∵点P在△ABC的中位线EF上,∴
=
.
∴
=
,即S1+S2=
S.
∴
S≥2
,当且仅当S1=S2=
S时取等号,此时S1S2取得最大值
S2.
此时点P为线段EF的中点.
以PB、PC为邻边作平行四边形PBDC,连接PD交BC于点O.
则
+
=
=2
=-2
,
化为
+
+
=
.
∵
+x
+y
=
,
∴x=y=
.
∴2x+3y=
.
故答案为:
.

∵点P在△ABC的中位线EF上,∴
| S△BPC |
| S |
| 1 |
| 2 |
∴
| S1+S2 |
| S |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| S1S2 |
| 1 |
| 4 |
| 1 |
| 16 |
此时点P为线段EF的中点.
以PB、PC为邻边作平行四边形PBDC,连接PD交BC于点O.
则
| PB |
| PC |
| PD |
| PO |
| PA |
化为
| PA |
| 1 |
| 2 |
| PB |
| 1 |
| 2 |
| PC |
| 0 |
∵
| PA |
| PB |
| PC |
| 0 |
∴x=y=
| 1 |
| 2 |
∴2x+3y=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题综合考查了向量的平行四边形法则、向量共面的基本定理、三角形的中位线定理、基本不等式的性质等基础知识与基本技能方法,属于难题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
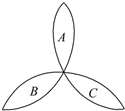 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则它在下列区间上不是减函数的是( )
| 3 |
| x |
| A、(0,+∞) |
| B、(-∞,0) |
| C、(-∞,0)∪(0,+∞) |
| D、(1,+∞) |
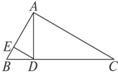 如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=