题目内容
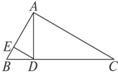 如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=考点:余弦定理
专题:三角函数的求值
分析:由Rt△ABD中,DE垂直于AB,得出△BDE与△DAE相似,由相似得比例求出DE的长,利用勾股定理求出AD的长,同理求出DC的长,在△ADC中,利用余弦定理即可求出AC的长.
解答:
解:∵在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,
∴∠EAD+∠ADE=90°,∠ADE+∠BDE=90°,
∴∠EAD=∠BDE,
∵∠AED=∠DEB=90°,
∴△AED∽△DEB,
∵AE=4,BE=1,
∴ED2=AE•BE=4,即ED=2,
根据勾股定理得:AD=
=2
,BD=
=
,
同理△ABD∽△CAD,即AD2=BD•DC,
∴DC=
=4
,
在△ADC中,利用余弦定理得:AC2=AD2+DC2-2AD•DC•cos∠ADC=20+80-0=100,
则AC=10.
故答案为:10
∴∠EAD+∠ADE=90°,∠ADE+∠BDE=90°,
∴∠EAD=∠BDE,
∵∠AED=∠DEB=90°,
∴△AED∽△DEB,
∵AE=4,BE=1,
∴ED2=AE•BE=4,即ED=2,
根据勾股定理得:AD=
| AE2+ED2 |
| 5 |
| DE2+BE2 |
| 5 |
同理△ABD∽△CAD,即AD2=BD•DC,
∴DC=
(2
| ||
|
| 5 |
在△ADC中,利用余弦定理得:AC2=AD2+DC2-2AD•DC•cos∠ADC=20+80-0=100,
则AC=10.
故答案为:10
点评:此题考查了余弦定理,相似三角形的判定与性质,以及勾股定理,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
i为虚数单位,复平面内表示复数z=
的点在( )
| 1 |
| i-1 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 某同学在7天内每天参加体育锻炼的时间(单位:分钟)用茎叶图表示如图,图中左列表示时间的十位数,右列表示时间的个位数.则这7天该同学每天参加体育锻炼时间(单位:分钟)的平均数为
某同学在7天内每天参加体育锻炼的时间(单位:分钟)用茎叶图表示如图,图中左列表示时间的十位数,右列表示时间的个位数.则这7天该同学每天参加体育锻炼时间(单位:分钟)的平均数为