题目内容
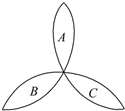 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:n次独立重复试验中恰好发生k次的概率
专题:概率与统计
分析:根据条件先求出逆时针和顺时针跳的概率,然后根据跳4次回到A,则应满足两次逆时针,两次顺时针,根据概率公式即可得到结论.
解答:
解:设按照顺时针跳的概率为p,则逆时针方向跳的概率为2p,则p+2p=3p=1,
解得p=
,即按照顺时针跳的概率为
,则逆时针方向跳的概率为
,
若青蛙在A叶上,则跳四次之后停在A叶上,
则满足四次跳跃中有2次是顺时针方向跳,有2次是逆时针跳,
①若先按逆时针开始从A→B,则剩余3次中有1次是按照逆时针,其余2次按顺时针跳,则对应的概率为
×
×
×(
)2=
=
,
②若先按顺时针开始从A→C,则剩余3次中有1次是按照顺时针,其余2次按逆时针跳,则对应的概率为
×
×
×(
)2=
=
,
则概率为
+
=
,
故选:B
解得p=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
若青蛙在A叶上,则跳四次之后停在A叶上,
则满足四次跳跃中有2次是顺时针方向跳,有2次是逆时针跳,
①若先按逆时针开始从A→B,则剩余3次中有1次是按照逆时针,其余2次按顺时针跳,则对应的概率为
| 2 |
| 3 |
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 12 |
| 81 |
| 4 |
| 27 |
②若先按顺时针开始从A→C,则剩余3次中有1次是按照顺时针,其余2次按逆时针跳,则对应的概率为
| 1 |
| 3 |
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 12 |
| 81 |
| 4 |
| 27 |
则概率为
| 4 |
| 27 |
| 4 |
| 27 |
| 8 |
| 27 |
故选:B
点评:本题主要考查概率的计算,利用独立重复试验的概率公式是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
从1、2、3、4这四个数中一次随机取两个,则取出的这两数字之和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
i为虚数单位,复平面内表示复数z=
的点在( )
| 1 |
| i-1 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知a0=20.5,b=log32,c=log20.1,则( )
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<c<a |