题目内容
已知函数y=f(x)=-x+1,y=g(x)=x2-bx(b>0)
(1)画出函数y=f(x)=-x+1的图象;
(2)当x>0时,y=f(x)与y=g(x)至少有一个函数值大于0,求b的取值范围.
(1)画出函数y=f(x)=-x+1的图象;
(2)当x>0时,y=f(x)与y=g(x)至少有一个函数值大于0,求b的取值范围.
考点:二次函数的性质,函数的图象
专题:函数的性质及应用
分析:(1)函数y=f(x)=-x+1为一次函数,图象为一条直线,确定直线上两个点后,可得函数图象;
(2)若x>0时,y=f(x)与y=g(x)至少有一个函数值大于0,结合(1)中函数图象可得仅须当x≥1时,y=g(x)=x2-bx>0恒成立即可,进而由二次函数的图象和性质可得b的取值范围.
(2)若x>0时,y=f(x)与y=g(x)至少有一个函数值大于0,结合(1)中函数图象可得仅须当x≥1时,y=g(x)=x2-bx>0恒成立即可,进而由二次函数的图象和性质可得b的取值范围.
解答:
解:(1)函数y=f(x)=-x+1的图象为一条直线
过点(0,1)和(1,0)
故函数y=f(x)=-x+1的图象如下图所示:

(2)当0<x<1时,y=f(x)>0,
若当x>0时,y=f(x)与y=g(x)至少有一个函数值大于0,
仅须当x≥1时,y=g(x)=x2-bx>0恒成立即可
∵当x>b时,g(x)=x2-bx>0恒成立
故b<1
即b的取值范围为0<b<1
即b的取值范围为(0,1)
过点(0,1)和(1,0)
故函数y=f(x)=-x+1的图象如下图所示:

(2)当0<x<1时,y=f(x)>0,
若当x>0时,y=f(x)与y=g(x)至少有一个函数值大于0,
仅须当x≥1时,y=g(x)=x2-bx>0恒成立即可
∵当x>b时,g(x)=x2-bx>0恒成立
故b<1
即b的取值范围为0<b<1
即b的取值范围为(0,1)
点评:本题考查的知识点是二次函数的性质,函数的图象,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合U={a,b,c,d,e},M={a,d},N={a,c,e},则M∪∁UN为( )
| A、{c,e} |
| B、{a,b,d} |
| C、{b,d} |
| D、{a,c,d,e} |
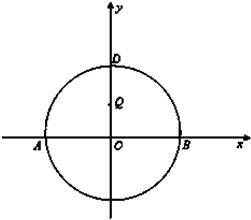 如图,AB为圆O直径,已知A(-2,0)、B(2,0),D为圆O上的一点,且
如图,AB为圆O直径,已知A(-2,0)、B(2,0),D为圆O上的一点,且