题目内容
在平面之间坐标系中,已知A(-1,1),B(2,4),圆C:x2-2ax+y2-4y+a2+
=0
(1)若圆C过点A,求a的值;
(2)若圆C与直线AB相交于P,Q两点,且CP⊥CQ,求a的值;
(3)若圆C与线段AB有公共点,求a的最小值.
| 51 |
| 25 |
(1)若圆C过点A,求a的值;
(2)若圆C与直线AB相交于P,Q两点,且CP⊥CQ,求a的值;
(3)若圆C与线段AB有公共点,求a的最小值.
考点:直线与圆的位置关系,圆的一般方程
专题:直线与圆
分析:(1)圆C过点A,代入圆的方程直接求解a的值;
(2)通过圆C与直线AB相交于P,Q两点,且CP⊥CQ,转化为,圆心到直线的距离与半径的关系,即可求a的值;
(3)若圆C与线段AB有公共点,列出不等式,即可求a的最小值.
(2)通过圆C与直线AB相交于P,Q两点,且CP⊥CQ,转化为,圆心到直线的距离与半径的关系,即可求a的值;
(3)若圆C与线段AB有公共点,列出不等式,即可求a的最小值.
解答:
解:(1)若圆C过点A,可得:(-1)2+2a+1-4+a2+
=0,可得a=-1±
;
(2)圆C与直线AB相交于P,Q两点,且CP⊥CQ,可知,圆心到直线的距离与半径满足r=
d,
A(-1,1),B(2,4),所以AB的方程为:x-y+2=0,
圆C:x2-2ax+y2-4y+a2+
=0,圆心(a,2),半径为:
.
∴d=
,则
×
=
,
可得a=±
;
(3)圆C与线段AB有公共点,可得:
≤
,可得-
≤a≤
,
a的最小值为:-
.
| 51 |
| 25 |
2
| ||
| 5 |
(2)圆C与直线AB相交于P,Q两点,且CP⊥CQ,可知,圆心到直线的距离与半径满足r=
| 2 |
A(-1,1),B(2,4),所以AB的方程为:x-y+2=0,
圆C:x2-2ax+y2-4y+a2+
| 51 |
| 25 |
| 7 |
| 5 |
∴d=
| |a| | ||
|
| 2 |
| |a| | ||
|
| 7 |
| 5 |
可得a=±
| 7 |
| 5 |
(3)圆C与线段AB有公共点,可得:
| |a| | ||
|
| 7 |
| 5 |
7
| ||
| 5 |
7
| ||
| 5 |
a的最小值为:-
7
| ||
| 5 |
点评:本题考查圆的一般方程与仔细的综合应用,直线与圆的位置关系,考查计算能力.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
已知平面向量
=(1,2),
=(x,1),如果向量
+2
与2
-
平行,那么
•(
-
)等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、-2 | ||
| B、-1 | ||
C、
| ||
D、
|
等差数列{an}中,a1=1,a2=3,数列{
}的前n项和为
,则n的值为( )
| 1 |
| anan+1 |
| 15 |
| 31 |
| A、15 | B、16 | C、17 | D、18 |
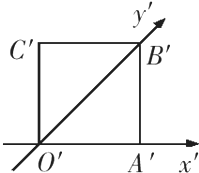 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )
一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )