题目内容
在△ABC中,已知A(1,-1),B(0,4),C(4,0).
(1)求BC边上的中线所在的直线方程;
(2)求△ABC的面积.
(1)求BC边上的中线所在的直线方程;
(2)求△ABC的面积.
考点:直线的一般式方程
专题:直线与圆
分析:(1)利用中点坐标公式、点斜式即可得出;
(2)利用点到直线的距离公式可得:点B到中线AM的距离d=
.利用两点之间的距离公式可得|AM|=
,再利用△ABC的面积S=2×
×d×|AM|即可得出.
(2)利用点到直线的距离公式可得:点B到中线AM的距离d=
| |0-4-4| | ||
|
| (1-2)2+(-1-2)2 |
| 1 |
| 2 |
解答:
解:(1)线段BC的中点为M(2,2),∴BC边上的中线所在的直线方程为y+1=
(x-1),化为3x-y-4=0;
(2)点B到中线AM的距离d=
=
.
|AM|=
=
,
∴△ABC的面积S=2×
×d×|AM|=
×
=8.
| -1-2 |
| 1-2 |
(2)点B到中线AM的距离d=
| |0-4-4| | ||
|
4
| ||
| 5 |
|AM|=
| (1-2)2+(-1-2)2 |
| 10 |
∴△ABC的面积S=2×
| 1 |
| 2 |
4
| ||
| 5 |
| 10 |
点评:本题考查了中点坐标公式、点斜式、点到直线的距离公式、两点之间的距离公式、三角形的面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=xα,α∈{-1,
,1,2,3},若f(x)是区间(-∞,+∞)上的增函数,则α的所有可能取值为( )
| 1 |
| 2 |
| A、{1,3} | ||
B、{
| ||
| C、{1,2,3} | ||
D、{-1,
|
已知函数f(x)=sin(2x+φ)在区间[
,
]上单调递减,则实数φ的取值可以是( )
| π |
| 3 |
| 5π |
| 6 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC的内角A,B,C对应的边分别为a,b,c,且
=
,则△ABC为( )
| c |
| a |
| cosB |
| 1+cosA |
| A、等边三角形 |
| B、等腰直角三角形 |
| C、直角三角形 |
| D、三边均不相等的三角形 |
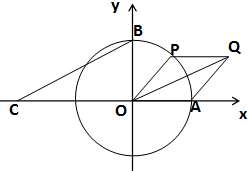 如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.