题目内容
14.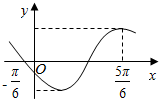 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.(1)求函数f(x)的表达式;
(2)求函数f(x)在[$\frac{3π}{2}$,2π]上的最大值和最小值.
分析 (1)首先,根据所给的图象,确定其周期,然后,代入相应的点即可得到相应的解析式;
(2)结合(1)和所给的范围,利用三角函数的单调性,确定其最大值和最小值.
解答 解:(1)根据题意,得
$\frac{3}{4}$T=$\frac{5π}{6}$-(-$\frac{π}{6}$),
∵T=$\frac{2π}{ω}$,
∴ω=$\frac{3}{2}$,
∴f(x)=2sin($\frac{3}{2}$x+φ),
∵f($\frac{5π}{6}$)=2,
∴sin($\frac{3}{2}×\frac{5π}{6}$+φ)=1,
∴sin($π+\frac{π}{4}$+φ)=1,
∴-sin($\frac{π}{4}$+φ)=1,
∵π<φ<$\frac{3π}{2}$,
∴φ=$\frac{5π}{4}$,
∴f(x)=2sin($\frac{3}{2}$x+$\frac{5π}{4}$),
(2)∵x∈[$\frac{3π}{2}$,2π],
∴$\frac{9π}{4}$≤$\frac{3}{2}$x≤3π,
∴$\frac{7π}{2}$≤$\frac{3}{2}$x+$\frac{5π}{4}$≤4π+$\frac{π}{4}$,
∴函数f(x)在[$\frac{3π}{2}$,2π]上的最大值$\sqrt{2}$,最小值-2.
点评 本题重点考查了三角函数的周期性、单调性、最值问题,掌握三角函数的图象与性质是解题的关键,属于中档题.

练习册系列答案
相关题目
4.函数f(x)=cosx,x∈[0,2π]与直线y=1所围区域的面积为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
19.下列说法正确的是( )
| A. | 命题“若x2<1,则-l≤x<l”的逆否命题是“若x2≥1,则x<-1或x≥l” | |
| B. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0” | |
| C. | “a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件 | |
| D. | 若“p∨q”为真命题,则p,q中至少有一个为真命题 |
6.已知函数f(x)=min$\{3-\frac{1}{2}{log_2}x,{log_2}x\}$,其中min(p,q}表示p,q两者中较小的一个,则满足f(x)<1的x的集合为( )
| A. | (0,$\sqrt{2}$) | B. | (0,$\sqrt{2}$)∪(4,+∞) | C. | (0,2) | D. | (0,2)∪(16,+∞) |