题目内容
6.已知函数f(x)=min$\{3-\frac{1}{2}{log_2}x,{log_2}x\}$,其中min(p,q}表示p,q两者中较小的一个,则满足f(x)<1的x的集合为( )| A. | (0,$\sqrt{2}$) | B. | (0,$\sqrt{2}$)∪(4,+∞) | C. | (0,2) | D. | (0,2)∪(16,+∞) |
分析 先根据“设min{p,q}表示p,q两者中的较小的一个”求得函数f(x),再按分段函数用分类讨论解不等式.
解答 解:①当3-$\frac{1}{2}$log2x<log2x时,
即 x>4时f(x)=3-$\frac{1}{2}$log2x,
②当3-$\frac{1}{2}$log2x>log2x时,
即x<4时f(x)=log2x,
∴f(x)<1;
当x>4时,
f(x)=3-$\frac{1}{2}$log2x<1,
此时:x>16;
当x<4时f(x)=log2x<1,
此时:0<x<2;
综上不等式的解集为:(0,2)∪(16,+∞).
故选:D.
点评 本题是一道新定义题,首先要根据定义求得函数,再应用函数解决相关问题,这类问题的解决,正确转化是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知非零向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a$•$\overrightarrow b$=0,且|$\overrightarrow a$-$\overrightarrow b$|=2|$\overrightarrow a$|,则向量$\overrightarrow a$-$\overrightarrow b$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
16.设偶函数f(x)在(-∞,0)上是增函数,且f(-$\frac{1}{2}$)=0,则不等式$\frac{f(x)+f(-x)}{2x}<0$的解集为( )
| A. | (-$\frac{1}{2}$,0)∪($\frac{1}{2}$,+∞) | B. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$)∪(0,$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
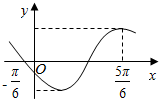 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.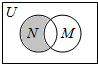 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.