题目内容
19.下列说法正确的是( )| A. | 命题“若x2<1,则-l≤x<l”的逆否命题是“若x2≥1,则x<-1或x≥l” | |
| B. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0” | |
| C. | “a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件 | |
| D. | 若“p∨q”为真命题,则p,q中至少有一个为真命题 |
分析 直接写出命题的逆否命题判断A;写出全程命题的否定判断B;举反例说明C错误,由复合命题的真假判定判断D正确.
解答 解:命题“若x2<1,则-l≤x<l”的逆否命题是“若x<-1或≥1,则x2≥1”,A错误;
命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0”,B错误;
当a=0时,g(x)=(ax-1)x=-x,“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”;
∴“a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件错误;
若“p∨q”为真命题,则p,q中至少有一个为真命题,正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了命题的否定与逆否命题,训练了充分必要条件的判定方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.“m<5”是“|m|<5”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
(1)若某人一月份应缴纳此项税款为280元,那么他当月的工资、薪金所得是多少?
(2)假设某人一个月的工资、薪金所得是x元(0<x≤10000),试将其当月应缴纳此项税款y元表示成关于x的函数.
| 全月应纳税所得额 | 税率(%) |
| 不超过1500元的部分 | 3 |
| 超过1500元至4500元的部分 | 10 |
| 超过4500元至9000元的部分 | 20 |
(2)假设某人一个月的工资、薪金所得是x元(0<x≤10000),试将其当月应缴纳此项税款y元表示成关于x的函数.
7.已知等比数列前n项和为Sn,若S2=4,S4=16,则S6=( )
| A. | 52 | B. | 64 | C. | -64 | D. | -52 |
4.已知R是实数集,M=$\{x|\frac{2}{x}<1\},N=\{y|y={x^2}-1\},则({C_R}M)∩N$=( )
| A. | (-1,2) | B. | [一l,2] | C. | (0,2) | D. | [0,2] |
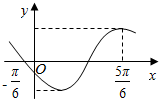 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.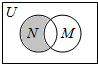 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.