题目内容
3.已知实数x、y满足$\left\{\begin{array}{l}{x≥0,y≥0}\\{2x-y+2≥0}\\{2x-y-3≤0}\\{x+y≤4}\end{array}\right.$,求z=3x+2y的最大值与最小值.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x≥0,y≥0}\\{2x-y+2≥0}\\{2x-y-3≤0}\\{x+y≤4}\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x+y=4}\\{2x-y-3=0}\end{array}\right.$,解得B($\frac{7}{3},\frac{5}{3}$),
又O(0,0),
化目标函数z=3x+2y为$y=-\frac{3}{2}x+\frac{z}{2}$.
由图可知,当直线$y=-\frac{3}{2}x+\frac{z}{2}$过O时,直线在y轴上的截距最小,z有最小值为0;
当直线$y=-\frac{3}{2}x+\frac{z}{2}$过B时,直线在y轴上的截距最大,z有最大值为$3×\frac{7}{3}+2×\frac{5}{3}=\frac{31}{3}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,考查数学转化思想方法,是中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
13.设R为实数集,集合S={x|log2x>0},T={x|x2>4},则S∩(∁RT)=( )
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
13.对于函数f(x)=sinx+cosx,下列命题是真命题的是( )
| A. | ?x∈R,f(x)=f(x+π) | B. | .?x∈R,f(x)=$\frac{5}{3}$ | C. | .?x∈R,f(x)=-1 | D. | ?x∈R,f(x)<$\sqrt{2}$ |
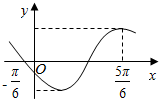 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.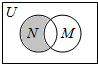 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.