题目内容
4.直线3x+4y-7=0的点方向式方程是$\frac{x-1}{4}$=$\frac{y-1}{-3}$;点法向式方程是3(x-1)+4(y-1)=0.分析 根据直线3x+4y-7=0求出它的法向量与方向向量,从而写出它的点方向式方程与点法式方程.
解答 解:因为直线3x+4y-7=0的法向量是$\overrightarrow{m}$=(3,4),
所以直线的一个方向向量为(4,-3);
又因为直线过点A(1,1),
所以直线的点方向式方程为:$\frac{x-1}{4}$=$\frac{y-1}{-3}$;
点法式方程为3(x-1)+4(y-1)=0.
故答案为:$\frac{x-1}{4}$=$\frac{y-1}{-3}$,3(x-1)+4(y-1)=0.
点评 本题考查了直线方程的应用问题,也考查了平面向量的应用问题,是基础题目.

练习册系列答案
相关题目
16.设偶函数f(x)在(-∞,0)上是增函数,且f(-$\frac{1}{2}$)=0,则不等式$\frac{f(x)+f(-x)}{2x}<0$的解集为( )
| A. | (-$\frac{1}{2}$,0)∪($\frac{1}{2}$,+∞) | B. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$)∪(0,$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
13.对于函数f(x)=sinx+cosx,下列命题是真命题的是( )
| A. | ?x∈R,f(x)=f(x+π) | B. | .?x∈R,f(x)=$\frac{5}{3}$ | C. | .?x∈R,f(x)=-1 | D. | ?x∈R,f(x)<$\sqrt{2}$ |
14.函数y=2|3-x|的值域是( )
| A. | (0,+∞) | B. | (0,1) | C. | (0,1] | D. | [1,+∞) |
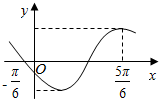 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.