题目内容
9.求适合下列条件的椭圆的标准方程:(Ⅰ)a=$\sqrt{6}$,b=1,焦点在x轴上;
(Ⅱ)焦点在y轴上,焦距是4,且经过点M(-2$\sqrt{6}$,3).
分析 根据椭圆的类型,确定几何量,即可求出椭圆的标准方程.
解答 解:(Ⅰ)a=$\sqrt{6}$,b=1,焦点在x轴上,椭圆的标准方程:$\frac{{x}^{2}}{6}+{y}^{2}$=1…(5分)
(Ⅱ)设椭圆的标准方程:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$,
∵焦距是4,且经过点M(-2$\sqrt{6}$,3),
∴$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}=4}\\{\frac{9}{{a}^{2}}+\frac{24}{{b}^{2}}=1}\end{array}\right.$,
∴a=6,b=4$\sqrt{2}$,
∴椭圆的标准方程$\frac{{y}^{2}}{36}+\frac{{x}^{2}}{32}=1$…(10分)
点评 本题考查椭圆的标准方程,考查学生的计算能力,根据椭圆的类型,确定几何量是关键.

练习册系列答案
相关题目
19.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0)(x1≠x2),都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0.则下列结论正确的是( )
| A. | f(0.32)<f(20.3)<f(log25) | B. | f(log25)<f(20.3)<f(0.32) | ||
| C. | f(log25)<f(0.32)<f(20.3) | D. | f(0.32)<f(log25)<f(20.3) |
20.等比数列{an}中,若S6=9,前3项和S3=8,则数列{an}的公比为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1或$\frac{1}{2}$ | D. | 1或2 |
1.已知非零向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a$•$\overrightarrow b$=0,且|$\overrightarrow a$-$\overrightarrow b$|=2|$\overrightarrow a$|,则向量$\overrightarrow a$-$\overrightarrow b$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
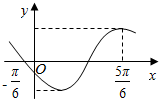 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.